Question

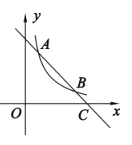
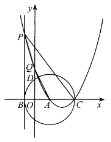
【题目】如图，在平面直角坐标系中，的半径为5，点A的坐标为(3，0)，与x轴相交于点B，C，交y轴正半轴于点D．

（1）求点B，D的坐标；

（2）过点B作的切线，与过点A，C的抛物线交于点P．抛物线交y轴正半轴于点Q．若P的纵坐标为t，四边形PQAC的面积为y．

①求y与t的函数关系式；

②若△PBO与△DOA相似，求取最小值时m的值．

Answer 1

【答案】（1），；（2）①，②16

【解析】

（1）根据的半径为5，点A的坐标为(3，0)，可求出点B的坐标，根据勾股定理可求出OD的长，即可求出点D的坐标；

（2）①设过，的抛物线的解析式为．由其过点，可求得抛物线的解析式为：，从而求出点Q的坐标及OQ的长，

由四边形PQAC的面积=，即可求出y与t的函数关系式；

②分两种情况：当和当，根据相似三角形的性质列出关于t的方程，求出t的值，从而求出y的值，即可求出取最小值时m的值.

（1）∵的半径为5，点A的坐标为(3，0)，与x轴相交于点B，C，

∴点B的坐标为，点C的坐标为（8,0），

∵OA=3，AD=5，

∴，

∴D点坐标为（0,4），

（2）①设过，的抛物线的解析式为．

抛物线过点，

∴，

，

∴抛物线的解析式为：．

，即．

∴；

②若，

∴，即，

可得，

∵，

∴．

．

当时，有最小值为．

若，

∴，即，

可得，

此时．

．

当时，有最小值为．

，

取最小值时，的值为16.