题目内容
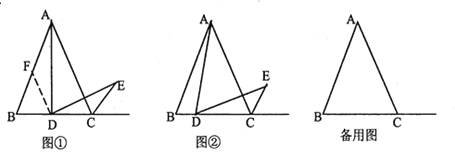
【题目】(1)(问题情境)小明遇到这样一个问题:
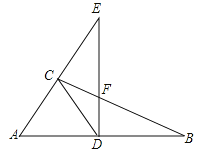
如图①,已知![]() 是等边三角形,点
是等边三角形,点![]() 为
为![]() 边上中点,
边上中点,![]() ,
,![]() 交等边三角形外角平分线
交等边三角形外角平分线![]() 所在的直线于点
所在的直线于点![]() ,试探究
,试探究![]() 与
与![]() 的数量关系.
的数量关系.
小明发现:过![]() 作
作![]() ,交
,交![]() 于
于![]() ,构造全等三角形,经推理论证问题得到解决.请直接写出
,构造全等三角形,经推理论证问题得到解决.请直接写出![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(2)(类比探究)
如图②,当![]() 是线段
是线段![]() 上(除
上(除![]() 外)任意一点时(其他条件不变)试猜想
外)任意一点时(其他条件不变)试猜想![]() 与
与![]() 的数量关系并证明你的结论.
的数量关系并证明你的结论.
(3)(拓展应用)
当![]() 是线段
是线段![]() 上延长线上,且满足
上延长线上,且满足![]() (其他条件不变)时,请判断
(其他条件不变)时,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() 是等边三角形,理由见解析.
是等边三角形,理由见解析.
【解析】
(1)根据等边三角形的性质可得![]() ,然后根据平行线的性质可得
,然后根据平行线的性质可得![]() ,从而证出
,从而证出![]() 是等边三角形,即可证出
是等边三角形,即可证出![]() ,然后证出
,然后证出![]() 、
、![]() ,最后利用ASA即可证出
,最后利用ASA即可证出![]() ,从而得出结论;
,从而得出结论;
(2)过![]() 作
作![]() 交
交![]() 于
于![]() ,同理可知
,同理可知![]() 是等边三角形,从而证出
是等边三角形,从而证出![]() ,再证出
,再证出![]() 和
和![]() ,利用ASA即可证出
,利用ASA即可证出![]() ,从而得出结论;
,从而得出结论;
(3)根据等三角形的性质和已知条件可得![]() ,再根据三线合一可得
,再根据三线合一可得![]() 垂直平分
垂直平分![]() ,从而得出
,从而得出![]() ,再根据等边三角形的判定即可证出结论.
,再根据等边三角形的判定即可证出结论.
解:(1)![]() ,理由如下:
,理由如下:
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 外角平分线,
外角平分线,
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴在![]() 与
与![]() 中,
中,
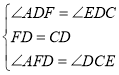
∴![]() ,
,
∴![]() ;
;
(2)![]()
证明:过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
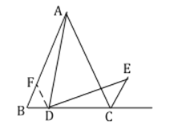
∵![]() 是等边三角形,
是等边三角形,
∴![]() 是等边三角形,
是等边三角形,
∴BF=BD
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∵![]() 是
是![]() 外角平分线,
外角平分线,
∴![]() ,
,
∴![]() ,
,
∴![]()
在![]() 与
与![]() 中,
中,
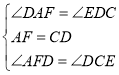
∴![]() ,
,
∴![]() ;
;
(3)![]() 是等边三角形,
是等边三角形,
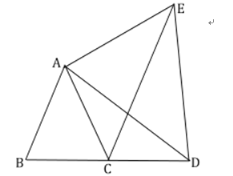
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是等边三角形外角平分线.
是等边三角形外角平分线.
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形.
是等边三角形.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目