Question

如图，⊙O1与⊙O2相交于A、B两点，若AB=O1A=4，O2A=2.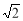

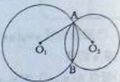
求：（1）∠O1AO2的度数；（2）O1与O2之间的距离。

Answer 1

（1）∠O1AO2的度数为105°；（2）O1与O2之间的距离为2+2

【解析】

试题分析：（1）连接O2B，可证明△ABO2是等腰直角三角形，从而可知∠BAO2=45°，连接O1O2，则O1O2⊥AB于C，可求出∠BAO1=60°，进而可知：∠O1AO2的度数为105°；

（2）由勾股定理可求出O1C，O2C的长度，从而可求出O1O2的值.

试题解析：（1）连接O2B，

∵O2A=2

∴O2B=2

∵O2A2+ O2B2=16=42=AB2

∴△O2AB是等腰直角三角形，

∴∠O2AB=45°

连接O1O2，则O1O2⊥AB，

∴AC=AB=2

在Rt△AO1C中，

cos∠O1AB=

∴∠O1AB=60°

∴∠O1AO2=∠O1AB+∠O2AB=60°+45°=105°；

(2)在Rt△AO1C中，

O1C=

在Rt△AO2B中

O2C=AB=2

∴O1O2=O1C+O2C=.

考点：两圆相交的问题.