题目内容
如图,![]() 已知抛物线
已知抛物线![]() 与y轴交于点A,与x轴交于点B(-1,0)和点C(3,0).
与y轴交于点A,与x轴交于点B(-1,0)和点C(3,0).
(1)求抛物线的表达式和对称轴;
(2)设抛物线的对称轴与直线AC交于点D,连接AB、BD,求△ABD的面积;
![]() (3)点M为抛物线上一动点,过点M作y轴
(3)点M为抛物线上一动点,过点M作y轴![]() 的平行线M
的平行线M![]() N,与直线AC交于点N.问在抛物线上是否存在点M,使得以D、N、M为顶点的三角形与△ACO相似?若存在,求点
N,与直线AC交于点N.问在抛物线上是否存在点M,使得以D、N、M为顶点的三角形与△ACO相似?若存在,求点![]() M的坐标;若不存在,请说明理由。
M的坐标;若不存在,请说明理由。
 |
.解:(1)∵抛物线![]() 经过B(-1,0)和C(3,0)
经过B(-1,0)和C(3,0)
∴![]() 解得
解得![]()
∴抛物线的表达式为![]()
∴对称轴为直线x=1 …………………………………………………3分
(2)令x=0得y=3 ∴A(0,3)
设AC的解析式为y=kx+b将A(0,3)、C(3,0)代入得
![]()
∴直线AC的解析式为y=-x+3
当x=1时,y=2 ∴D(1,2)
∴![]() …………6分
…………6分
(3)假设存在点M,使得以D、M、N为顶点的三角形与△AOC相似。
在Rt△AOC中,∵OA=OC=3,∴Rt△AOC为等腰直角三角形,
∴∠OAC=∠OCA=45°,则以D、M、N为顶点的三角形也必须是等腰直角三角形。
由MN∥OA得∠MND=∠OAC=45°,故以D、M、N为顶点的直角三角形只能以点D或M为直角顶点。…………………………………………………………7分
①当M为直角顶点时,DM⊥MN,此时△DMN∽△COA,∴DM所在的直线为y=2
由![]() 解得x=1±
解得x=1±![]() ,∴M(
,∴M(![]() 或M(
或M(![]() 。………9分
。………9分
②当D为直角顶点时,DM⊥AC,此时△DMN∽△OCA
∵D在对称轴上,∴DB=DC,∴∠DBC=∠DCB=450,∴∠ BDC=900,∴BD⊥AC,
故M在直线BD上。…………10分
设BD的解析式为y=kx+b,将B、D的坐标代入得![]()
∴BD的解析式为y=x+1
由![]() 。将x=-1代入y=x+1得y=0 ,∴M(-1,0)
。将x=-1代入y=x+1得y=0 ,∴M(-1,0)
将x=2代入y=x+1得y=3,∴M(2,3)
综上所述,在抛物线上存在点M,使得以D、N、M为顶点的三角形与△ACO相似,点M的坐标为(![]() ,(
,(![]() ,(-1,0),(2,3)
,(-1,0),(2,3)

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案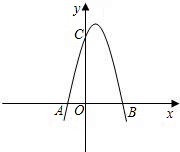 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).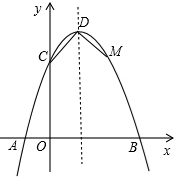 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1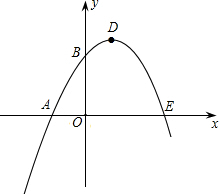 函数的最大值是4.
函数的最大值是4. (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )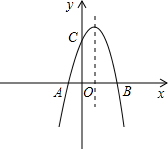 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).