题目内容
小明喜欢研究问题,他将一把三角板的直角顶点放在平面直角坐标系的原点O处,两条直角边与抛物线y=ax2(a<0)交于A、B两点.(1)如图1,当OA=OB=2时,则a=______
【答案】分析:(1)根据二次函数图象的对称性以及等腰直角三角形的性质求出点A的坐标,然后代入函数解析式,计算即可求出a的值;
(2)根据OC=1可知点B的横坐标为1,再根据二次函数解析式求出点B的纵坐标,从而得到BC的长度,再过点A作推出AD⊥x轴于点D,然后推出△DAO与△COB相似,然后设出点A的坐标并表示出OD、AD的长度,根据相似三角形对应边成比例列出比例式进行计算即可得解;
(3)根据二次函数解析式,设点A、B的坐标分别为A(m,- m2)、B(n,-
m2)、B(n,- n2),根据相似三角形对应边成比例列式求出mn=2,再利用待定系数法列式求出直线AB的解析式,根据解析式的常数项是常数-
n2),根据相似三角形对应边成比例列式求出mn=2,再利用待定系数法列式求出直线AB的解析式,根据解析式的常数项是常数- 即可得解.
即可得解.
解答:解:(1)∵OA=OB=2,
∴等腰Rt△AOB关于y轴对称,
∴点A的坐标为(- ,-
,- ),
),
∴a(- )2=-
)2=- ,
,
解得a=- ;
;
(2)由(1)可知抛物线的解析式为y=- x2,
x2,
∵OC=1,
∴yB=- ,
,
∴B(1,- ),
),
过点A作AD⊥x轴于点D,又BC⊥x轴于点C,
 ∴∠ADO=∠BCO=90°,
∴∠ADO=∠BCO=90°,
∴∠1+∠2=90°,
∵AO⊥OB,
∴∠1+∠3=90°,
∴∠2=∠3,
∴△DAO∽△COB,
∴ =
= ,
,
设点A坐标为(x,- x2),则OD=-x,AD=-
x2),则OD=-x,AD=- x2,
x2,
∴ =
= ,
,
解得x=-2,
∴yA=-2 ,
,
故点A的坐标为(-2,-2 );
);
(3)定点坐标是(0,- ).
).
理由如下:根据(1)的结论,设点A、B的坐标为A(m,- m2)、B(n,-
m2)、B(n,- n2),
n2),
根据(2)△DAO∽△COB,
∴ =
= ,
,
即 =
= ,
,
整理得,mn=-2,
设直线AB的解析式为y=kx+b,
则 ,
,
解得 ,
,
∴b=-2× =-
=- ,
,
∴三角板绕点O旋转任意角度时,直线AB的倾斜发生变化,但总是与y轴相交于点(0,- ),
),
即线段AB总经过一个定点(0,- ).
).
点评:本题是对二次函数的综合考查,有等腰直角三角形的性质,坐标与图形的变化,相似三角形的判定与性质,旋转变换的性质,待定系数法求函数解析式,综合性较强,难度较大.
(2)根据OC=1可知点B的横坐标为1,再根据二次函数解析式求出点B的纵坐标,从而得到BC的长度,再过点A作推出AD⊥x轴于点D,然后推出△DAO与△COB相似,然后设出点A的坐标并表示出OD、AD的长度,根据相似三角形对应边成比例列出比例式进行计算即可得解;
(3)根据二次函数解析式,设点A、B的坐标分别为A(m,-
 m2)、B(n,-
m2)、B(n,- n2),根据相似三角形对应边成比例列式求出mn=2,再利用待定系数法列式求出直线AB的解析式,根据解析式的常数项是常数-
n2),根据相似三角形对应边成比例列式求出mn=2,再利用待定系数法列式求出直线AB的解析式,根据解析式的常数项是常数- 即可得解.
即可得解.解答:解:(1)∵OA=OB=2,
∴等腰Rt△AOB关于y轴对称,
∴点A的坐标为(-
 ,-
,- ),
),∴a(-
 )2=-
)2=- ,
,解得a=-
 ;
;(2)由(1)可知抛物线的解析式为y=-
 x2,
x2,∵OC=1,
∴yB=-
 ,
,∴B(1,-
 ),
),过点A作AD⊥x轴于点D,又BC⊥x轴于点C,
 ∴∠ADO=∠BCO=90°,
∴∠ADO=∠BCO=90°,∴∠1+∠2=90°,
∵AO⊥OB,
∴∠1+∠3=90°,
∴∠2=∠3,
∴△DAO∽△COB,
∴
 =
= ,
,设点A坐标为(x,-
 x2),则OD=-x,AD=-
x2),则OD=-x,AD=- x2,
x2,∴
 =
= ,
,解得x=-2,
∴yA=-2
 ,
,故点A的坐标为(-2,-2
 );
);(3)定点坐标是(0,-
 ).
).理由如下:根据(1)的结论,设点A、B的坐标为A(m,-
 m2)、B(n,-
m2)、B(n,- n2),
n2),根据(2)△DAO∽△COB,
∴
 =
= ,
,即
 =
= ,
,整理得,mn=-2,
设直线AB的解析式为y=kx+b,
则
 ,
,解得
 ,
,∴b=-2×
 =-
=- ,
,∴三角板绕点O旋转任意角度时,直线AB的倾斜发生变化,但总是与y轴相交于点(0,-
 ),
),即线段AB总经过一个定点(0,-
 ).
).点评:本题是对二次函数的综合考查,有等腰直角三角形的性质,坐标与图形的变化,相似三角形的判定与性质,旋转变换的性质,待定系数法求函数解析式,综合性较强,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 处,两条直角边与抛物线
处,两条直角边与抛物线 交于
交于 、
、 两点.
两点.  时,则
时,则 = ;
= ;
 轴于点
轴于点 ,测得
,测得 ,求出此时点
,求出此时点
 处,两条直角边与抛物线
处,两条直角边与抛物线 交于
交于 、
、 两点.
两点.  时,则
时,则 = ;
= ;
 轴于点
轴于点 ,测得
,测得 ,求出此时点
,求出此时点
 处,两条直角边与抛物线
处,两条直角边与抛物线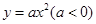 交于
交于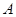 、
、 两点.
两点.  时,则
时,则 = ;
= ;
 轴于点
轴于点 ,测得
,测得 ,求出此时点
,求出此时点