Question

如图，在离树BC12米的A处，用测角仪测得树顶的仰角是30°，测角仪AD高为1.5米，求树高BC．（计算结果可保留根号）

Answer 1

分析：本题是一个直角梯形的问题，可以通过点D作DE⊥BC于E，把求CB的问题转化求BE的长，从而可以在△BDE中利用三角函数．

解答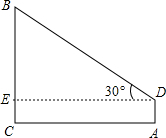：解：过点D作DE⊥BC于E，则四边形DECA是矩形，
∴DE=AC=12米．CE=AD=1.5米．
在直角△BED中，∠BDE=30° tan30°=

BE

DE

，
∴BE=DE•tan30°=4

3

米．
∴BC=BE+CE=4

3

+

3

2

米．

点评：解直角梯形可以通过作高线转化为解直角三角形和矩形的问题．