题目内容
若(a+2)2+|2b-1|=0,则a2006•b2007=________.

分析:由题意(a+2)2+|2b-1|=0,根据非负数的性质可以求出a和b的值,然后代入a2006•b2007求解.
解答:∵(a+2)2+|2b-1|=0,
∴a+2=0,2b-1=0,
∴a=-2,b=
 ,
,∴a2006•b2007=(ab)2006×b=
 ,
,故答案为
 .
.点评:此题主要考查非负数绝对值和偶次方的性质即所有非负数都大于等于0,本题是一道基础题.

练习册系列答案
相关题目
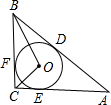 如图,⊙O内切于Rt△ABC,∠C=Rt∠,D、E、F是切点,若∠BOC=105°,AB=4cm,则∠OBC=
如图,⊙O内切于Rt△ABC,∠C=Rt∠,D、E、F是切点,若∠BOC=105°,AB=4cm,则∠OBC=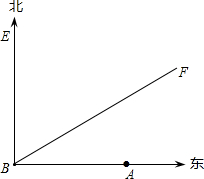 如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.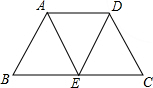 在等腰梯形ABCD中,AD∥BC,E是BC的中点,连接AE,DE,AE与DE相等吗?
在等腰梯形ABCD中,AD∥BC,E是BC的中点,连接AE,DE,AE与DE相等吗? 13、如图,在△ABC中,AB=AC,AB的中垂线交AB于点D,交BC的延长线于点E,交AC于点F,若∠A=50°,AB+BC=6,则△BCF的周长=
13、如图,在△ABC中,AB=AC,AB的中垂线交AB于点D,交BC的延长线于点E,交AC于点F,若∠A=50°,AB+BC=6,则△BCF的周长=