Question

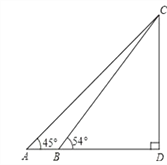
【题目】如图， AB、BC的垂直平分线交于点P，

(1)求证：PA= PC.

(2)连接AC，

①若∠ABC=150°，证明△PAC是等边三角形.

②若∠ABC= °，△PAC是等腰直角三角形.（直接填结果，不需要说明）

Answer 1

【答案】（1）证明见解析；（2）①证明见解析；②135°

【解析】试题分析：（1）由垂直平分线的性质即可得到结论；

（2）①根据有一个角为60°的等腰三角形是等边三角形进行判断；

②由等腰三角形的性质得到∠A=∠ABP，∠C=∠PBC，再由四边形内角和等于360°可以求出当∠APC=90°时，∠ABC的度数．

试题解析：解：（1）连接PB．∵边AB，BC的垂直平分线交于点P，∴PA=PB，PB=PC，∴PA=PB=PC．

（2）①∵∠ABC=150°，∴∠A＋∠C=150°，∴∠APC=360°―150°―150°=60°，∵PA=PC

∴△PAC是等边三角形．

②∵PA=PB，∴∠A=∠PBA，∵PB=PC，∴∠C=∠PBC，∵∠A+∠ABC+∠C+∠APC=360°，∴2∠ABC+∠APC=360°，∵∠APC=90°，∴2∠ABC=270°，∴∠ABC=135°．