题目内容
如图，A在DE上，F在DC上，且∠1=∠2=∠3，AC=CE，则DE的等于（ ）| A、DC | B、BC | C、AB | D、AC |
分析：根据∠1=∠3证明得到∠ACB=∠ECD，再根据∠2=∠3证明得到∠D=∠B，然后利用“角角边”定理证明△ABC与△EDC全等，根据全等三角形对应边相等即可证明．
解答：解：∵∠1=∠3，
∴∠1+∠ACD=∠3+∠ACD，
即∠ACB=∠ECD，
∵∠2=∠3，
∴180°-∠2-∠AFD=180°-∠3-∠BFC，
即∠B=∠D，
在△ABC与△EDC中，
，
∴△ABC≌△EDC（AAS），
∴DE=AB．
故选C．
∴∠1+∠ACD=∠3+∠ACD，
即∠ACB=∠ECD，
∵∠2=∠3，
∴180°-∠2-∠AFD=180°-∠3-∠BFC，
即∠B=∠D，
在△ABC与△EDC中，
|
∴△ABC≌△EDC（AAS），
∴DE=AB．
故选C．
点评：本题考查了全等三角形的判定与性质，全等三角形的证明方法一般有“边边边”，“边角边”，“角边角”，“角角边”四种，直角三角形还有“斜边、直角边”，熟练掌握判定方法是解题的关键．
练习册系列答案
相关题目
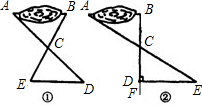育人中学初一（1）班学生到野外活动，为测量一池塘两端A、B的距离，设计了如下两种方案：
如图，A在DE上，F在DC上，且∠1=∠2=∠3，AC=CE，则DE的等于