题目内容
 如图,长方形ABCD中,AB=3,BC=4,若将该矩形折叠,使点C与点A重合,则折痕EF的长为( )
如图,长方形ABCD中,AB=3,BC=4,若将该矩形折叠,使点C与点A重合,则折痕EF的长为( )分析:如图,过点E作EH⊥BC于H,根据轴对称的性质就可以求出AG=CD,AF=CF,GE=DE,∠G=∠D=90°,∠GAF=∠C=90°.由矩形的性质和勾股定理就可以求出DE,再由△ABF∽△AGE,就可以求出BF的值,在Rt△FHE中由勾股定理就可以求出EF的值.
解答:解:如图,过点E作EH⊥BC于H,
∴∠EHC=∠EHF=90°.
∵四边形ABCD是矩形,
∴∠B=∠C=∠D=∠BAD=90°,AB=CD,AD=BC,
∵AB=3,BC=4,
∴CD=3,AD=4
∴∠EHC=∠C=∠D=90°,
∴四边形EHCD是矩形,
∴EH=CD,ED=CH.
∵四边形AFEG与四边形CFED关于EF对称,
∴四边形AFEG≌四边形CFED
∴AG=CD=3,AF=CF,GE=DE,∠G=∠D=90°,∠GAF=∠C=90°.
设ED=x,则GE=x,AE=4-x,在Rt△AGE中,由勾股定理,得
9+x2=(4-x)2,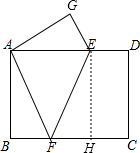
解得:x=
,
∴AE=
.
∵∠GAE+∠FAE=∠FAE+∠BAF=90°,
∴∠GAE=∠BAF.
∵∠G=∠B=90°,
∴△ABF∽△AGE,
∴
=
,
∴
=
,
∴BF=
.
∴FH=4-
-
=
.
在Rt△FHE中,由勾股定理,得
EF=
.
故选B.
∴∠EHC=∠EHF=90°.
∵四边形ABCD是矩形,
∴∠B=∠C=∠D=∠BAD=90°,AB=CD,AD=BC,
∵AB=3,BC=4,
∴CD=3,AD=4
∴∠EHC=∠C=∠D=90°,
∴四边形EHCD是矩形,
∴EH=CD,ED=CH.
∵四边形AFEG与四边形CFED关于EF对称,
∴四边形AFEG≌四边形CFED
∴AG=CD=3,AF=CF,GE=DE,∠G=∠D=90°,∠GAF=∠C=90°.
设ED=x,则GE=x,AE=4-x,在Rt△AGE中,由勾股定理,得
9+x2=(4-x)2,

解得:x=
| 7 |
| 8 |
∴AE=
| 25 |
| 8 |
∵∠GAE+∠FAE=∠FAE+∠BAF=90°,
∴∠GAE=∠BAF.
∵∠G=∠B=90°,
∴△ABF∽△AGE,
∴
| AB |
| AG |
| BF |
| GE |
∴
| 3 |
| 3 |
| BF | ||
|
∴BF=
| 7 |
| 8 |
∴FH=4-
| 7 |
| 8 |
| 7 |
| 8 |
| 9 |
| 4 |
在Rt△FHE中,由勾股定理,得
EF=
| 15 |
| 4 |
故选B.
点评:本题考查了轴对称的性质的运用,勾股定理的运用,矩形的判定及性质的运用,解答时灵活运用勾股定理求解是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (15届江苏初二1试)已知:如图,长方形ABCD被两条线段分割成四个小长方形,如果其中图形Ⅰ、Ⅱ、Ⅲ的面积依次为8、6、5,则阴影部分的面积为
(15届江苏初二1试)已知:如图,长方形ABCD被两条线段分割成四个小长方形,如果其中图形Ⅰ、Ⅱ、Ⅲ的面积依次为8、6、5,则阴影部分的面积为 9、如图,长方形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果∠BAF=50°,则∠EAF的度数为( )
9、如图,长方形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果∠BAF=50°,则∠EAF的度数为( ) 已知如图:长方形ABCD中,AB=3,BC=4,将△BCD沿BD翻折,点C落在点F处.
已知如图:长方形ABCD中,AB=3,BC=4,将△BCD沿BD翻折,点C落在点F处. 如图,长方形ABCD中放置9个形状、大小都相同的小长方形,小长方形的长为x,宽为y(尺寸如图)
如图,长方形ABCD中放置9个形状、大小都相同的小长方形,小长方形的长为x,宽为y(尺寸如图)