题目内容
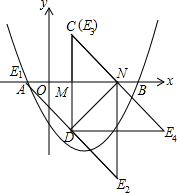
 如图,在平面直角坐标系中,抛物线y=ax2+bx-2与x轴交于点A(-1,0)、B(4,0).点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.
如图,在平面直角坐标系中,抛物线y=ax2+bx-2与x轴交于点A(-1,0)、B(4,0).点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m. (1)求这条抛物线所对应的函数关系式.
(2)求点C在这条抛物线上时m的值.
(3)将线段CN绕点N逆时针旋转90°后,得到对应线段DN.当点D在这条抛物线的对称轴上时,求点D的坐标.
考点:二次函数综合题
专题:
分析:(1)将A(-1,0)、B(4,0)两点的坐标代入y=ax2+bx-2,运用待定系数法即可求出抛物线的解析式;
(2)先根据等腰直角三角形的性质求出点C的坐标为(m,2),再将C的坐标代入y=
x2-
x-2,即可求出m的值;
(3)先由旋转的性质得出点D的坐标为(m,-2),再根据二次函数的性质求出抛物线y=
x2-
x-2的对称轴为直线x=
,然后根据点D在直线x=
上,即可求出点D的坐标;
(2)先根据等腰直角三角形的性质求出点C的坐标为(m,2),再将C的坐标代入y=
| 1 |
| 2 |
| 3 |
| 2 |
(3)先由旋转的性质得出点D的坐标为(m,-2),再根据二次函数的性质求出抛物线y=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:(1)∵抛物线经过点A(-1,0)、B(4,0),
∴
解得
∴抛物线所对应的函数关系式为y=
x2-
x-2;
(2)∵△CMN是等腰直角三角形CMN,∠CMN=90°,
∴CM=MN=2,
∴点C的坐标为(m,2),
∵点C(m,2)在抛物线上,
∴
m2-
m-2=2,
解得m1=
,m2=
.
∴点C在这条抛物线上时,m的值为
或
;
(3)∵将线段CN绕点N逆时针旋转90°后,得到对应线段DN,
∴∠CND=90°,DN=CN=
CM=
MN,
∴CD=
CN=2CM=2MN,
∴DM=CM=MN,∠DMN=90°,
∴点D的坐标为(m,-2).
又∵抛物线y=
x2-
x-2的对称轴为直线x=
,点D在这条抛物线的对称轴上,
∴点D的坐标为(
,-2);
∴
|
解得
|
∴抛物线所对应的函数关系式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)∵△CMN是等腰直角三角形CMN,∠CMN=90°,
∴CM=MN=2,
∴点C的坐标为(m,2),
∵点C(m,2)在抛物线上,
∴
| 1 |
| 2 |
| 3 |
| 2 |
解得m1=
3+
| ||
| 2 |
3-
| ||
| 2 |
∴点C在这条抛物线上时,m的值为
3+
| ||
| 2 |
3-
| ||
| 2 |

(3)∵将线段CN绕点N逆时针旋转90°后,得到对应线段DN,
∴∠CND=90°,DN=CN=
| 2 |
| 2 |
∴CD=
| 2 |
∴DM=CM=MN,∠DMN=90°,
∴点D的坐标为(m,-2).
又∵抛物线y=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴点D的坐标为(
| 3 |
| 2 |
点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求抛物线的解析式,二次函数的性质,等腰直角三角形的性质,旋转的性质等知识,综合性较强,难度适中.

练习册系列答案
相关题目
下列事件中,必然事件是( )
| A、掷一枚硬币,着地时反面向上 |
| B、星期天一定是晴天 |
| C、打开电视机,正在播放动画片 |
| D、在标准大气压下,水加热到100℃会沸腾 |
二次函数y=3(x+1)2+2的顶点坐标为( )
| A、(-1,-2) |
| B、(-1,2) |
| C、(1,-2) |
| D、(1,2) |
点P(2,3)关于原点的对称点Q的坐标是( )
| A、(-2,3) |
| B、(2,-3) |
| C、(3,2) |
| D、(-2,-3) |