题目内容
将1,- ,
, ,-
,- ,
, ,-
,- ,…按一定规律排列如图:
,…按一定规律排列如图:
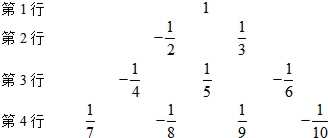
…请你写出第6行从左至右第3个数是________.
-
分析:观察各行的规律,分三部分分析:分数符号的规律,即当分母是奇数时,为正号.当分母是偶数时,符号是负号.所有的分子都是1.分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n= .根据这一规律,即可得出答案.
.根据这一规律,即可得出答案.
解答:∵分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n= .
.
根据这一规律,计算第5行末尾数的分母是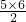 =15,
=15,
则第6行从左至右第3个数的分母是15+3=18,
则该分数是- .
.
故答案为:- .
.
点评:此题主要考查了数字变化规律,根据分母的奇偶性确定该数的符号.本题的关键规律为:分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n= .
.

分析:观察各行的规律,分三部分分析:分数符号的规律,即当分母是奇数时,为正号.当分母是偶数时,符号是负号.所有的分子都是1.分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n=
 .根据这一规律,即可得出答案.
.根据这一规律,即可得出答案.解答:∵分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n=
 .
.根据这一规律,计算第5行末尾数的分母是
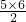 =15,
=15,则第6行从左至右第3个数的分母是15+3=18,
则该分数是-
 .
.故答案为:-
 .
.点评:此题主要考查了数字变化规律,根据分母的奇偶性确定该数的符号.本题的关键规律为:分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n=
 .
. 
练习册系列答案
相关题目
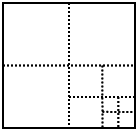 将一个边长为1的正方形纸片,剪成四个大小一样的正方形,然后将其中一个小正方形再按照同样的方法剪成四个正方形,如此循环下去,观察下列图表,回答下列问题:
将一个边长为1的正方形纸片,剪成四个大小一样的正方形,然后将其中一个小正方形再按照同样的方法剪成四个正方形,如此循环下去,观察下列图表,回答下列问题:| 操作次数 | 1 | 2 | 3 | 4 | … |
| 所得正方形的总个数 | 4 | 7 | 10 | 13 | … |
(2)从表格和第(1)题的结果中你发现了什么?我发现
(3)请你根据你的发现归纳出:当操作次数为n次时,得到的正方形的个数是
(4)仔细观察图形,请你利用图形揭示的规律进行下面的计算(要有揭示规律的过程):
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 256 |
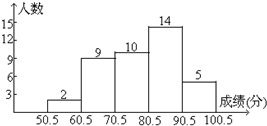 高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题:
高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题: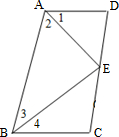 22、如图,四边形ABCD中,点E在边CD上,连接AE、BE,给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB,将其中的三个关系式作为题设,另外两个作为结论,便构成一个命题.
22、如图,四边形ABCD中,点E在边CD上,连接AE、BE,给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB,将其中的三个关系式作为题设,另外两个作为结论,便构成一个命题.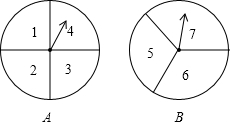 小亮获胜.
小亮获胜.