Question

已知关于x的方程x²+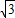kx+k²-k+2=0，为判别这个方程根的情况，一名同学的解答过程如下：
“解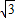：△=（k）²-4×1×（k²-k+2）
=-k²+4k-8
=（k-2）²+4．
∵（k-2）²≥0，4＞0，∴△=（k-2）²+4＞0．
∴原方程有两个不相等的实数根．”
请你判断其解答是否正确，若有错误，请你写出正确解答．

Answer 1

【答案】分析：此题注意在配方时别丢负号；一元二次方程根的情况取决于判别式△，当△＞0时，方程有两个不相等的实数根，当△=0时，方程有两个相等的实数根，当△＜0时，方程无实数根．
解答：解：解答过程不正确，
△=-k²+4k-8=-（k²-4k+8）
=-[（k-2）²-4+8]
=-（k-2）²-4
∵（k-2）²≥0，
∴-（k-2）²≤0
∴-（k-2）²-4＜0
即△＜0，所以方程没有实数根．
点评：本题考查一元二次方程根的判别式与配方的知识．解题时要注意解题过程中的负号别漏掉．