题目内容
在△ABC中,AC=BC,∠C=90°,将一块三角板的直角顶点放在斜边AB的中点P处,将三角板绕P点旋转,三角板的两直角边分别交AC、CB于D、E两点,如图①、②所示.
问PD与PE有何大小关系?在旋转过程中,还会存在与图①、②不同的情形吗?若存在,请在图③中画出,并选择图②或图③为例加以证明,若不存在请选择图②加以证明.

问PD与PE有何大小关系?在旋转过程中,还会存在与图①、②不同的情形吗?若存在,请在图③中画出,并选择图②或图③为例加以证明,若不存在请选择图②加以证明.
分析:根据图形判断出四边形CEPD是正方形,再根据正方形的四条边都相等解答;
根据点D、E的位置判断出还有不同的情形,然后过点P作PM⊥AC于M,作PN⊥BC于N,根据点P是AB的中点判断出四边形MCNP是正方形,根据正方形的性质可得PM=PN,∠MPN=90°,再根据同角的余角相等求出∠DPM=∠EPN,然后利用“角边角”证明△PDM和△PEN全等,根据全等三角形对应边相等证明即可.
根据点D、E的位置判断出还有不同的情形,然后过点P作PM⊥AC于M,作PN⊥BC于N,根据点P是AB的中点判断出四边形MCNP是正方形,根据正方形的性质可得PM=PN,∠MPN=90°,再根据同角的余角相等求出∠DPM=∠EPN,然后利用“角边角”证明△PDM和△PEN全等,根据全等三角形对应边相等证明即可.
解答: 解:PD=PE.
解:PD=PE.
还有不同的情形如图③;
过点P作PM⊥AC于M,作PN⊥BC于N,
∵点P是AB的中点,AC=BC,∠C=90°,
∴四边形MCNP是正方形,
∴PM=PN,∠MPN=90°,
∵∠DPM+∠MPE=∠DPE=90°,
∠EPN+∠MPE=∠MPN=90°,
∴∠DPM=∠EPN,
在△PDM和△PEN中,
,
∴△PDM≌△PEN(ASA),
∴PD=PE.
 解:PD=PE.
解:PD=PE.还有不同的情形如图③;
过点P作PM⊥AC于M,作PN⊥BC于N,
∵点P是AB的中点,AC=BC,∠C=90°,
∴四边形MCNP是正方形,
∴PM=PN,∠MPN=90°,
∵∠DPM+∠MPE=∠DPE=90°,
∠EPN+∠MPE=∠MPN=90°,
∴∠DPM=∠EPN,
在△PDM和△PEN中,
|
∴△PDM≌△PEN(ASA),
∴PD=PE.
点评:考查了全等三角形的判定与性质,等腰直角三角形的性质,正方形的判定与性质,作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
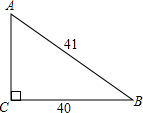 如图,在△ABC中,AC=
如图,在△ABC中,AC= 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=