Question

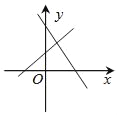
【题目】如图，在平面直角坐标系中有一正方形AOBC，反比例函数y= 经过正方形AOBC对角线的交点，半径为（6﹣3 ）的圆内切于△ABC，则k的值为 ．

Answer 1

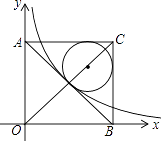
【答案】9
【解析】解：设正方形对角线交点为D，过点D作DM⊥AO于点M，DN⊥BO于点N，设圆心为Q，切点为H、E，连接QH、QE．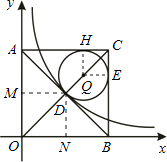
∵在正方形AOBC中，反比例函数y= 经过正方形AOBC对角线的交点，
∴AD=BD=DO=CD，NO=DN，HQ=QE，HC=CE，
∵QH⊥AC，QE⊥BC，∠ACB=90°，
∴四边形HQEC是正方形．
∵半径为（6﹣3 ）的圆内切于△ABC，
∴DO=CD．
∵HQ2+HC2=QC2 ，
∴2HQ2=QC2=2×（6﹣3 ）2 ，
∴QC2=108﹣72 =（6 ﹣6）2 ，
∴QC=6 ﹣6，
∴CD=6 ﹣6+（6﹣3 ）=3 ，
∴DO=3 ．
∵NO2+DN2=DO2=（3 ）2=18，
∴2NO2=18，
∴NO2=9，
∴DNNO=9，
即：xy=k=9．
所以答案是9．
【考点精析】认真审题，首先需要了解正方形的性质(正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)，还要掌握三角形的内切圆与内心(三角形的内切圆的圆心是三角形的三条内角平分线的交点，它叫做三角形的内心)的相关知识才是答题的关键．