题目内容
已知△ABC中,AB=AC,∠ADB=∠AEC,且∠ADB+∠BAC=180°
(1)当∠BAC=90°时,线段EC、BD、DE之间的数量关系为 EC=BD+DE (不证明);
(2)当∠BAC=60°时,线段EC、BD、DE之间的数量关系为______,猜想结论,并且加以证明;
(3)当∠BAC=120°时,画出满足题意的图形,并且猜想线段EC、BD、DE之间的数量关系______(不证明).
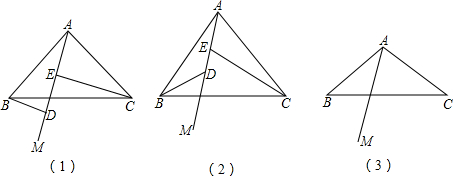
解:(2)如图2,EC=BD+DE.
∵∠ADB+∠BAC=180°,且∠BAC=60°,
∴∠ADB=120°,
∴∠1+∠ABD=60°.
∵∠1+∠2=60°,
∴∠ABD=∠2.
在△ABD和△CAE中,
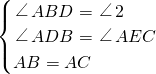 ,
,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE.
∵AD=DE+AE,
∴CE=DE+BD;
(3)如图2,EC=BD+DE,
∵∠ADB+∠BAC=180°,且∠BAC=120°,
∴∠ADB=60°,
∴∠1+∠ABD=120°.
∵∠1+∠2=120°,
∴∠ABD=∠2.
在△ABD和△CAE中,
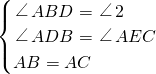 ,
,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE.
∵AD=DE+AE,
∴CE=DE+BD.
故答案为:CE=DE+BD,CE=DE+BD.
分析:(2)如图2,EC=BD+DE,由∠ADB+∠BAC=180°及∠BAC=60°就可以求出∠ADB=120°,由条件可以得出△ABD≌△CAE,由全等三角形的性质就可以得出结论;
(3)如图2,EC=BD+DE,由∠ADB+∠BAC=180°及∠BAC=120°就可以求出∠ADB=60°,由条件可以得出△ABD≌△CAE,由全等三角形的性质就可以得出结论.
点评:本题是结论猜想试题,考查了全等三角形的判定与性质的运用,解答时运用AB=AC构造全等三角形是解答本题的关键.
∵∠ADB+∠BAC=180°,且∠BAC=60°,
∴∠ADB=120°,
∴∠1+∠ABD=60°.
∵∠1+∠2=60°,
∴∠ABD=∠2.
在△ABD和△CAE中,
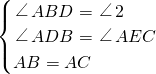 ,
,∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE.
∵AD=DE+AE,
∴CE=DE+BD;

(3)如图2,EC=BD+DE,
∵∠ADB+∠BAC=180°,且∠BAC=120°,
∴∠ADB=60°,
∴∠1+∠ABD=120°.
∵∠1+∠2=120°,
∴∠ABD=∠2.
在△ABD和△CAE中,
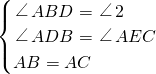 ,
,∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE.
∵AD=DE+AE,
∴CE=DE+BD.
故答案为:CE=DE+BD,CE=DE+BD.
分析:(2)如图2,EC=BD+DE,由∠ADB+∠BAC=180°及∠BAC=60°就可以求出∠ADB=120°,由条件可以得出△ABD≌△CAE,由全等三角形的性质就可以得出结论;
(3)如图2,EC=BD+DE,由∠ADB+∠BAC=180°及∠BAC=120°就可以求出∠ADB=60°,由条件可以得出△ABD≌△CAE,由全等三角形的性质就可以得出结论.
点评:本题是结论猜想试题,考查了全等三角形的判定与性质的运用,解答时运用AB=AC构造全等三角形是解答本题的关键.

练习册系列答案
相关题目
 如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程证明△ABD≌△ACD的理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程证明△ABD≌△ACD的理由. 已知△ABC中,AB=AC,AD为BC边上的中线,BE为AC边上的高,
已知△ABC中,AB=AC,AD为BC边上的中线,BE为AC边上的高, 如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程,说明△ABD≌△ACD的理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程,说明△ABD≌△ACD的理由.
 如图:已知△ABC中,AB=17cm,BC=30cm,BC边上的中线AD=8cm.求证:△ABC是等腰三角形.
如图:已知△ABC中,AB=17cm,BC=30cm,BC边上的中线AD=8cm.求证:△ABC是等腰三角形.