Question

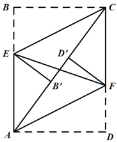
【题目】如图，在矩形ABCD中，点E、F分别在AB、CD边上，AD=6，AB=8，将△CBE沿CE翻折，使B点的对应点B′刚好落在对角线AC上，将△ADF沿AF翻折，使D点的对应点D′也恰好落在对角线AC上，连接EF，则EF的长为________．

Answer 1

【答案】

【解析】

过点F作FM⊥AB于点M，利用AA定理证得，从而求得，设，则，利用勾股定理列方程求得BE=3，AE=5，DF=3，CF=5，然后判定四边形MACF是矩形，求得EM= 2，MF =6，从而利用勾股定理使问题得解．

解：过点F作FM⊥AB于点M

由折叠可知，

又∵

∴

∴

设，则

∴在Rt中，

∴（舍去）

则BE=3，AE=5

同理DF=3，CF=5

∵FM⊥AB且四边形ABCD是矩形

∴四边形MACF是矩形

∴EM=EA-AM=EA-DF=5-3=2，MF=AD=BC=6

∴在Rt△EFM中，

故答案为：．