题目内容
如图15,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为![]() ,则tanA的值是 .
,则tanA的值是 .

![]()
解析:根据三角形内心的特点知∠ABO=∠CBO,∵已知点C、点B的坐标,
∴OB=OC,∠OBC=45°,∠ABC=90°可知△ABC为直角三角形,BC=2![]() ,
,
∵点A在直线AC上,设A点坐标为(x,![]() x-1),
x-1),
根据两点距离公式可得: AB2=x2+(![]() x-3)2, AC2=(x-2)2+(
x-3)2, AC2=(x-2)2+(![]() x-1)2,
x-1)2,
在Rt△ABC中, AB2+BC2=AC2,解得:x=-6,y=-4,∴AB=6![]() ,
,
∴tanA=![]() =
=![]() .
.

练习册系列答案
相关题目
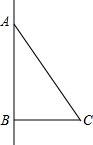 (2012•黄冈模拟)如图,Rt△ABC的两直角边AB=4cm,BC=3cm.以AB所在直线为轴,将△ABC旋转一周后所得几何体的侧面展开图的面积是
(2012•黄冈模拟)如图,Rt△ABC的两直角边AB=4cm,BC=3cm.以AB所在直线为轴,将△ABC旋转一周后所得几何体的侧面展开图的面积是 ,则tanA的值是 .
,则tanA的值是 . 
 ,则tanA的值是 .
,则tanA的值是 . 
 ,则tanA的值是 .
,则tanA的值是 . 