题目内容
 已知反比例函数y1=
已知反比例函数y1= (x>0)的图象经过点A(2,4).
(x>0)的图象经过点A(2,4).
(1)求k的值,并在平面直角坐标系中画出y1= (x>0)的图象;
(x>0)的图象;
(2)方程x2+bx-k=0的根可看做y1= 的图象与y2=x+b的图象交点的横坐标.
的图象与y2=x+b的图象交点的横坐标.
依此方法,若方程x2+bx-k=0的一个实根为m,且满足2<m<3,则b的取值范围为______;
(3)方程x3-x-1=0的实数根x0所在的范围是n<x0<n+1,根据以上经验,可求出正整数n的值为______.
 解:(1)将点A(2,4)代入反比例函数y1=
解:(1)将点A(2,4)代入反比例函数y1= 得,
得,k=2×4=8,
函数解析式为:y1=
 ;
;列表得:
| x | … | 1 | 2 | 4 | … |
| y | … | 8 | 4 | 2 | … |
(2)∵方程x2+bx-k=0的根可看做y1=
 的图象与y2=x+b的图象交点的横坐标,且方程x2+bx-k=0的一个实根为m,满足2<m<3,
的图象与y2=x+b的图象交点的横坐标,且方程x2+bx-k=0的一个实根为m,满足2<m<3,∴当x=2时,y1=
 =4,当x=3时,y1=
=4,当x=3时,y1= ,
,∴y1=
 的图象与y2=x+b的图象一个交点在点(2,4)与(3,
的图象与y2=x+b的图象一个交点在点(2,4)与(3, )之间,
)之间,∵当x=2,y=4时,2+b=4,
解得:b=2,
当x=3,y=
 时,3+b=
时,3+b= ,
,解得:b=-
 ,
,∴b的取值范围为:-
 <b<2;
<b<2; (3)∵方程x3-x-1=0,
(3)∵方程x3-x-1=0,∴x2-1=
 ,
,∴它的根可视为y=x2-1和y=
 的交点的横坐标,
的交点的横坐标,当x=1时,x2-1=0,
 =1,交点在x=1的右边,
=1,交点在x=1的右边,当x=2时,x2-1=3,
 =
= ,交点在x=2的左边,
,交点在x=2的左边,又∵交点在第一象限.
∴1<x0<2,
∵实数根x0所在的范围是n<x0<n+1,
∴n=1.
故答案为:(2)-
 <b<2,(3)1.
<b<2,(3)1.分析:(1)将点A(2,4)代入反比例函数解析式,即可求出k的值,从而得到反比例函数解析式.
(2)由方程x2+bx-k=0的一个实根为m,且满足2<m<3,易求得y1=
 的图象与y2=x+b的图象一个交点在点(2,4)与(3,
的图象与y2=x+b的图象一个交点在点(2,4)与(3, )之间,将其代入y2=x+b,即可求得b的取值范围;
)之间,将其代入y2=x+b,即可求得b的取值范围;(3)由方程x3-x-1=0,可得x2-1=
 ,则可得它的根可视为y=x2-1和y=
,则可得它的根可视为y=x2-1和y= 的交点的横坐标,继而求得实数根x0所在的范围是1<x0<2,则可求得答案.
的交点的横坐标,继而求得实数根x0所在的范围是1<x0<2,则可求得答案.点评:此题考查了反比例函数的性质、待定系数法求反比例函数的解析式以及函数与方程的关系等知识.此题难度较大,注意掌握方程思想、函数思想与数形结合思想的应用.

练习册系列答案
相关题目
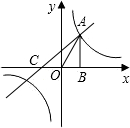 为1.过点A作AB⊥x轴于点B,△AOB的面积1.
为1.过点A作AB⊥x轴于点B,△AOB的面积1.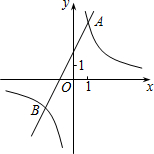 已知反比例函数y1=
已知反比例函数y1= 如图,已知反比例函数
如图,已知反比例函数 已知反比例函数
已知反比例函数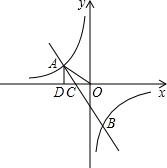 的横坐标为
的横坐标为