题目内容
已知α为锐角,下列结论①sin2α+cos2α=l;②如果α>45°,那么sinα>cosα;③如果cosα> ,那么α<60°;
,那么α<60°;
④ .正确的有________.
.正确的有________.
①②③④
分析:①根据同角的三角函数之间的关系即可判断;
②把余弦变成正弦,根据正弦函数随角度的增大而增大,即可作出判断;
③根据余弦函数随角度的增大而减小即可判断;
④根据正弦函数的函数值一定不大于1即可作出判断.
解答:①根据同角的三角函数之间的关系可得:sin2α+cos2α=l,正确;
②∵α>45°,
∴90°-α<α,而cosα=sin(90°-α),
∴sinα>sin(90°-α),
即sinα>cosα,故正确.
③∵cosα> =cos60°
=cos60°
∴α<60°,故正确.
④∵sinα≥1,
∴sinα-1≤0,
∴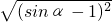 =|sinα-1|=1-sinα,故正确.
=|sinα-1|=1-sinα,故正确.
所以正确的是:①②③④.
故答案是:①②③④.
点评:本题主要考查了三角函数的增减性以及同角三角函数之间的关系,是需要熟记的内容.
分析:①根据同角的三角函数之间的关系即可判断;
②把余弦变成正弦,根据正弦函数随角度的增大而增大,即可作出判断;
③根据余弦函数随角度的增大而减小即可判断;
④根据正弦函数的函数值一定不大于1即可作出判断.
解答:①根据同角的三角函数之间的关系可得:sin2α+cos2α=l,正确;
②∵α>45°,
∴90°-α<α,而cosα=sin(90°-α),
∴sinα>sin(90°-α),
即sinα>cosα,故正确.
③∵cosα>
 =cos60°
=cos60°∴α<60°,故正确.
④∵sinα≥1,
∴sinα-1≤0,
∴
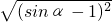 =|sinα-1|=1-sinα,故正确.
=|sinα-1|=1-sinα,故正确.所以正确的是:①②③④.
故答案是:①②③④.
点评:本题主要考查了三角函数的增减性以及同角三角函数之间的关系,是需要熟记的内容.

练习册系列答案
相关题目
已知α为锐角,下列结论:①sinα+cosα=1;②如果α>45°,那么sinα>cosα;③如果cosα>
,那么α<60°;④
=1-sinα,正确的有( )
| 1 |
| 2 |
| (sinα-1)2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知α为锐角,下列结论:
(1)sinα+cosα=1;
(2)若α>45°,则sinα>cosα;
(3)如果cosα>
,则α<60°;
(4)
=1-sinα.
其中正确结论的序号是( )
(1)sinα+cosα=1;
(2)若α>45°,则sinα>cosα;
(3)如果cosα>
| 1 |
| 2 |
(4)
| (sinα-1)2 |
其中正确结论的序号是( )
| A、(1)(3)(4) |
| B、(2)(4) |
| C、(2)(3)(4) |
| D、(3)(4) |
 ,则α<60°;
,则α<60°; =1-sinα.
=1-sinα. ,那么α<60°;④
,那么α<60°;④ =1-sinα,正确的有( )
=1-sinα,正确的有( )