题目内容
有一块厚度均匀的任意四边形木块，如图所示．如何用作图的方法来确定此木块的重心位置？请写出作图步骤．
分析：如图，先确定四边形ABCD中△ABC的重心P，△ACD的重心Q，△ABD点重心R，△BCD的重心S，则四边形PSQR的对角线的交点即为四边形ABCD的重心．
解答：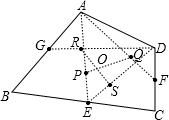
解：作图步骤：
（1）取AB、BC、CD三边的中点G、E、F，连接AE，AF，DE，DG；
（2）分别在AE，AF，DE，DG上取EP=
AE，FQ=
AF，ES=
DE，GR=
DG；
（3）连接PQ，RS交于O点．
O点即为所求．
解：作图步骤：（1）取AB、BC、CD三边的中点G、E、F，连接AE，AF，DE，DG；
（2）分别在AE，AF，DE，DG上取EP=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
（3）连接PQ，RS交于O点．
O点即为所求．
点评：本题考查了四边形重心的画法．关键是先作出四边形中各三角形的重心，四个重心所组成的四边形的对角线的交点即为原四边形的重心．
练习册系列答案
相关题目
有一块厚度均匀的任意四边形木块，如图所示．如何用作图的方法来确定此木块的重心位置？请写出作图步骤．