题目内容
某公园计划砌一个形如图1所示的喷水池，己知每个圆的半径为r，后来有人建议改为图2所示的形状，且外圆的直径不变，三个内圆的半径分别为
、
、
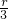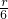，请你通过计算比较哪一种方案所砌水池的周边需要的材料多．
解：根据圆周长公式，得图1中，需要4πr；
图2中，中间的三个小圆的直径之和是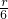：×2+×2+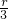×2=2r，所以需要4πr．
∴两种方案所砌水池的周边需要的材料一样多．
分析：根据圆的周长公式，将每个圆的周长计算出来，找到和周长L的关系即可．
点评：此题考查了圆的认识；解题时注意：第二个图中，计算三个小圆的周长时候，提取π，所有的直径之和是大圆的直径．
图2中，中间的三个小圆的直径之和是：
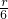×2+×2+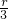×2=2r，所以需要4πr．∴两种方案所砌水池的周边需要的材料一样多．
分析：根据圆的周长公式，将每个圆的周长计算出来，找到和周长L的关系即可．
点评：此题考查了圆的认识；解题时注意：第二个图中，计算三个小圆的周长时候，提取π，所有的直径之和是大圆的直径．
练习册系列答案
相关题目
某公园计划砌一个形如图1所示的喷水池，己知每个圆的半径为r，后来有人建议改为图2所示的形状，且外圆的直径不变，三个内圆的半径分别为