Question

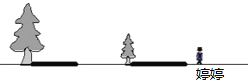
【题目】两棵树（大树和小树）在一盏路灯下的影子如图所示

（1）确定路灯灯泡的位置（用点P表示）和表示婷婷的影长的线段（用线段AB表示）．

（2）若小树高为2m，影长为4m；婷婷高1.5m，影长为4.5米，且婷婷距离小树10米，试求出路灯灯泡的高度．

Answer 1

【答案】（1）见解析（2）路灯灯泡的高度为10.5m

【解析】

（1）根据中心投影的特点可知，连接物体和它影子的顶端所形成的直线必定经过点光源．所以分别把两棵树的顶端和影子的顶端连接并延长可交于一点，即点光源的位置，连接PC并延长交QA的延长线与点B，即可得；
（2）由DF∥PQ得△DEF∽△QEP，根据相似三角形的性质有，即①，同理可得，即②，联立①②可得PQ．

（1）如图，点P即为灯泡所在位置；

线段AB即为婷婷的影长；

（2）如图，由题意知，DF=2，DE=4，DA=10，AC=1.5，AB=4.5，

∵DF∥PQ，

∴△DEF∽△QEP，

∴，即①，

∵CA∥PQ，

∴△CAB∽△PQB，

∴，即②，

由①②可得PQ=10.5，

答：路灯灯泡的高度为10.5m．