题目内容
如图，AB为⊙O的直径，CD是弦，sin∠CDB=| 3 | 5 |
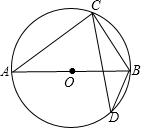
分析：由圆周角定理知∠A=∠CDB；在Rt△ACB中，可借助∠CDB的正弦值和BC的长，求出AB的值．
解答：解：∵AB是⊙O的直径，
∴∠ACB=90°．
Rt△ABC中，sinA=sin∠CDB=
，BC=6，
∴AB=BC÷sin∠CDB=6÷
=10．
∴∠ACB=90°．
Rt△ABC中，sinA=sin∠CDB=
| 3 |
| 5 |
∴AB=BC÷sin∠CDB=6÷
| 3 |
| 5 |
点评：此题主要考查了圆周角定理及解直角三角形的应用．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知⊙O的直AB=20cm，CD垂AB于E，CD=12cm，AE的长为（ ）| A、1cm | B、2cm | C、3cm | D、4cm |
如图，在水塔O的东北方向32m处有一抽水站A，在水塔的东南方向24m处有一建筑工地B，在AB间建一条直水管，则水管的长为
如图，已知⊙O的直AB=20cm，CD垂AB于E，CD=12cm，AE的长为