题目内容
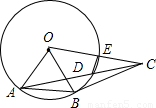
8、如图中，BC切圆O于B，AB=BC=OA，连AC交圆O于D，OC交圆O于E，则∠CED的度数为（ ）分析：由∠CED在圆的外部，所以尽可能让它成为圆内接四边形的外角，需在圆中构造四边形，利用已知条件，得出所有能得出的角度，只要求出圆内接四边形与∠CED有关的内角，即可求出∠CED的度数．
解答：解：延长CO到圆上一点m，连接mA
∵BC切圆O于B
∴∠OBC=90°
又∵AB=BC=OA
∴△OAB是等边三角形，∠BAC=∠BCA，
BO=BC，∴∠BOC=∠BCO=45°
又∵∠OBA=60°
∴∠BAC=∠BCA=15°
∵∠AOB=60°，∠BOC=45°
∴∠OmA=75°，
∵Om=0A
∴∠mAO=52.5°
∴∠mAC=97.5°
∴∠mAC=∠CED（圆内接四边形的外角等于它不相邻的内角）
故选：D
∵BC切圆O于B
∴∠OBC=90°
又∵AB=BC=OA
∴△OAB是等边三角形，∠BAC=∠BCA，
BO=BC，∴∠BOC=∠BCO=45°
又∵∠OBA=60°
∴∠BAC=∠BCA=15°
∵∠AOB=60°，∠BOC=45°
∴∠OmA=75°，
∵Om=0A
∴∠mAO=52.5°
∴∠mAC=97.5°
∴∠mAC=∠CED（圆内接四边形的外角等于它不相邻的内角）
故选：D
点评：此题主要考查了切线的性质，等腰三角形的性质，圆内接四边形的性质，综合性较强，有利于同学们综合能力的提升．
练习册系列答案
阅读快车系列答案
相关题目
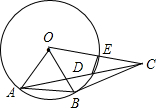如图中，BC切圆O于B，AB=BC=OA，连AC交圆O于D，OC交圆O于E，则∠CED的度数为
