题目内容
直角三角形中,两锐角的角平分线所夹的锐角是分析:根据△ACB为Rt△,利用三角形内角和定理求出∠CAB+∠ABC=90°,再利用角平分线的性质即可求出两锐角的角平分线所夹的锐角的度数.
解答:解:如图所示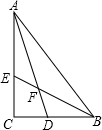
△ACB为Rt△,AD,BE,分别是∠CAB和∠ABC的角平分线,AD,BE相交于一点F.
∵∠ACB=90°,
∴∠CAB+∠ABC=90°
∵AD,BE,分别是∠CAB和∠ABC的角平分线,
∴∠FAB+∠FBA=
∠CAB+
∠ABC=45°.
故答案为:45.

△ACB为Rt△,AD,BE,分别是∠CAB和∠ABC的角平分线,AD,BE相交于一点F.
∵∠ACB=90°,
∴∠CAB+∠ABC=90°
∵AD,BE,分别是∠CAB和∠ABC的角平分线,
∴∠FAB+∠FBA=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:45.
点评:此题主要考查学生对三角形内角和定理和角平分线的性质等知识点的理解和掌握,此题难度不大,要求学生应熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目