Question

如图，点A、B、C、D在⊙O上，∠ADC=60°，C是弧AB的中点．
  
（1）判断△ABC的形状，并说明理由；
（2）若BC=cm，求图中阴影部分的面积．

Answer 1

（1）△ABC是等边三角形；（2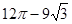）（）平方厘米

解析试题分析：（1）由C是弧AB的中点可得弧AC=弧BC，根据圆周角定理可得∠ADC=∠ABC=∠BAC=∠BDC=60°，即可得到△ABC的形状；
（2）连接BO、OC，过O作OE⊥BC于E，先根据垂径定理求得BE=EC=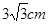，再根据圆周角定理可得∠BOC、∠BOE的度数，在Rt△BOE中，根据∠BOE的正弦函数可求得OB的长，再根据扇形的面积公式及三角形的面积公式求解即可.
（1）∵C是弧AB的中点，
∴弧AC=弧BC，
∴∠ADC=∠ABC=∠BAC=∠BDC=60°
∴∠ACB=60°，
∴AC=AB=BC，
∴△ABC是等边三角形；
（2）连接BO、OC，过O作OE⊥BC于E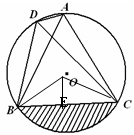

∵BC=，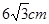
∴BE=EC=，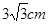
∵∠BAC=60°，
∴∠BOC=120°，
∴∠BOE=60°，在Rt△BOE中，sin60°=，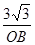
∴OB=6cm，
∴S扇形BOC=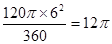cm²
∵S△BOC=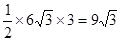cm²  
∴S阴影 =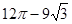cm² 
答：图中阴影部分的面积是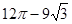（）平方厘米
考点：圆的综合题
点评：此类问题综合性强，难度较大，在中考中比较常见，一般作为压轴题，题目比较典型．