题目内容
已知α,β是关于x的二次方程x2+(2m-1)x+m2=0的二正根
(1)求m的取值范围;
(2)若α2+β2=49,求m的值.
解:(1)∵方程有二正根,
∴△=(2m-1)2-4m2≥0,
即4m≤1,
解得m≤ ,
,
又∵α>0,β>0,
∴α+β>0,αβ>0,
由根与系数的关系得,
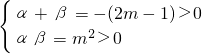 ,
,
解得m< 且m≠0,
且m≠0,
综上所述,m的取值范围是m≤ 且m≠0;
且m≠0;
(2)由α2+β2=49得,(α+β)2-2αβ=49,
由根与系数的关系可得方程(2m-1)2-2m2=49,
整理得,m2-2m-24=0,
即(m+4)(m-6)=0,
∴m+4=0,m-6=0,
解得m=-4或m=6,
又由(1)知m≤ 且m≠0,
且m≠0,
∴m=-4.
故答案为:(1)m≤ 且m≠0,(2)m=-4.
且m≠0,(2)m=-4.
分析:(1)先根据根的判别式求出m的取值范围,再根据两个根为正数,利用根与系数的关系列式求出m的取值范围,然后求它们的公共部分即可;
(2)先把α2+β2写出(α+β)2-2αβ的形式,再根据根与系数的关系列式解关于m的一元二次方程即可.
点评:本题考查了根的判别式与根与系数的关系,根据根的判别式与根与系数的关系列式是解题的关键,本题中先根据根的判别式求出m的取值范围容易漏掉而导致出错.
∴△=(2m-1)2-4m2≥0,
即4m≤1,
解得m≤
 ,
,又∵α>0,β>0,
∴α+β>0,αβ>0,
由根与系数的关系得,
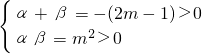 ,
,解得m<
 且m≠0,
且m≠0,综上所述,m的取值范围是m≤
 且m≠0;
且m≠0;(2)由α2+β2=49得,(α+β)2-2αβ=49,
由根与系数的关系可得方程(2m-1)2-2m2=49,
整理得,m2-2m-24=0,
即(m+4)(m-6)=0,
∴m+4=0,m-6=0,
解得m=-4或m=6,
又由(1)知m≤
 且m≠0,
且m≠0,∴m=-4.
故答案为:(1)m≤
 且m≠0,(2)m=-4.
且m≠0,(2)m=-4.分析:(1)先根据根的判别式求出m的取值范围,再根据两个根为正数,利用根与系数的关系列式求出m的取值范围,然后求它们的公共部分即可;
(2)先把α2+β2写出(α+β)2-2αβ的形式,再根据根与系数的关系列式解关于m的一元二次方程即可.
点评:本题考查了根的判别式与根与系数的关系,根据根的判别式与根与系数的关系列式是解题的关键,本题中先根据根的判别式求出m的取值范围容易漏掉而导致出错.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
已知x1、x2是关于x的一元二次方程x2-(2m+3)x+m2=0的两个不相等的实数根,且满足x1+x2=m2,则m的值是( )
| A、-1 | B、3 | C、3或-1 | D、-3或1 |