题目内容
如图将直线 向左平移m个单位,与双曲线
向左平移m个单位,与双曲线 交于点A,与x轴交于点B,则OB2-OA2+
交于点A,与x轴交于点B,则OB2-OA2+ AB2= .
AB2= .
【答案】分析:首先表示出平移后的直线解析式,设出点A的坐标,然后表示出所求代数式的值,再结合平移后的直线解析式以及双曲线的解析式进行解答.
解答:解:由题意知:平移后的直线解析式为:y= (x+m);
(x+m);
设A(x,y),易知:B(-m,0),则有:
OB2-OA2+ AB2=m2-(x2+y2)+
AB2=m2-(x2+y2)+ [(m+x)2+y2],联立y=
[(m+x)2+y2],联立y= (x+m),
(x+m),
整理得:原式=-2x2-2mx;
由于直线y= (x+m)与
(x+m)与 交于点A,联立两个函数解析式得:
交于点A,联立两个函数解析式得:
 (x+m)=-
(x+m)=- ,即x2+mx+2
,即x2+mx+2 =0,得-x2-mx=2
=0,得-x2-mx=2 ;
;
故所求代数式=-2x2-2mx=4 .
.
故答案为:4 .
.
点评:此题主要考查了函数图象的平移以及函数图象交点坐标的求法,难度适中,由于计算量较大,需要细心求解.
解答:解:由题意知:平移后的直线解析式为:y=
 (x+m);
(x+m);设A(x,y),易知:B(-m,0),则有:
OB2-OA2+
 AB2=m2-(x2+y2)+
AB2=m2-(x2+y2)+ [(m+x)2+y2],联立y=
[(m+x)2+y2],联立y= (x+m),
(x+m),整理得:原式=-2x2-2mx;
由于直线y=
 (x+m)与
(x+m)与 交于点A,联立两个函数解析式得:
交于点A,联立两个函数解析式得: (x+m)=-
(x+m)=- ,即x2+mx+2
,即x2+mx+2 =0,得-x2-mx=2
=0,得-x2-mx=2 ;
;故所求代数式=-2x2-2mx=4
 .
.故答案为:4
 .
.点评:此题主要考查了函数图象的平移以及函数图象交点坐标的求法,难度适中,由于计算量较大,需要细心求解.

练习册系列答案
相关题目
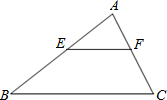 如图,在△ABC中,AE=EB,AF=FC,有一同学发现EF与BC存在以下关系:EF∥BC,且EF=
如图,在△ABC中,AE=EB,AF=FC,有一同学发现EF与BC存在以下关系:EF∥BC,且EF=

 已知一条直线经过A(0,4)、点B(2,0),如图.将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使DB=DC.求直线CD的函数解析式.
已知一条直线经过A(0,4)、点B(2,0),如图.将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使DB=DC.求直线CD的函数解析式. 如图将直线
如图将直线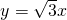 向左平移m个单位,与双曲线
向左平移m个单位,与双曲线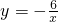 交于点A,与x轴交于点B,则OB2-OA2+
交于点A,与x轴交于点B,则OB2-OA2+ AB2=________.
AB2=________. 向左平移m个单位,与双曲线
向左平移m个单位,与双曲线 交于点A,与x轴交于点B,则OB2-OA2+
交于点A,与x轴交于点B,则OB2-OA2+ AB2= .
AB2= .