题目内容
【题目】如图，平面直角坐标系中，菱形OABC的边OA在x轴正半轴上，OA=10，cos∠COA=
．一个动点P从点O出发，以每秒1个单位长度的速度沿线段OA方向运动，过点P作PQ⊥OA，交折线段OC﹣CB于点Q，以PQ为边向右作正方形PQMN，点N在射线OA上，当P点到达A点时，运动结束．设点P的运动时间为t秒（t＞0）．
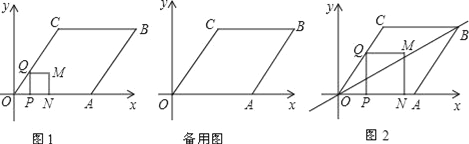
（1）C点的坐标为 ，当t= 时N点与A点重合；
（2）在整个运动过程中，设正方形PQMN与菱形OABC的重合部分面积为S，直接写出S与t之间的函数关系式和相应的自变量t的取值范围；
（3）如图2，在运动过程中，过点O和点B的直线将正方形PQMN分成了两部分，请问是否存在某一时刻，使得被分成的两部分中有一部分的面积是菱形面积的
？若存在，请求出对应的t的值；若不存在，请说明理由．
【答案】（1）t=
时，N点与A点重合；（2）①
，
②
，
③
，
④8＜t≤10，S=104﹣8t；
（3）①当0＜t≤6，
，
，
，
，
若
，则
，
，
若
，则
，
，
②当6＜t≤8，
，
，
，
，
若
，则
，t=0（舍），
若
，则
，t3=8；
③8＜t≤10，不存在符合条件的t值．
【解析】试题分析：（1）根据菱形的性质得出OA=OC，再根据三角函数求出点C的坐标即可；
（2）根据面积公式列出函数关系式，注意动点运动时的几种情况，得出自变量的取值范围；
（3）根据被分成的两部分中有一部分的面积是菱形面积的
，画出图示，分几种情况进行讨论解答．
试题解析：（1）∵菱形OABC中，OA=10，
∴OC=10，
∵cos∠COA=
，
∴点C的坐标为：（6，8），
∵动点P从点O出发，以每秒1个单位长度的速度沿线段OA方向运动，
∵OA=10，
∴t=时，N点与A点重合；
（2）①，
②，
③，
④8＜t≤10，S=104﹣8t；
（3）S菱形=80，直线OB过原点（0，0），B点（16，8），故直线OB解析式为
，
直线OB与PQ、MN分别交于E、F点，如图：
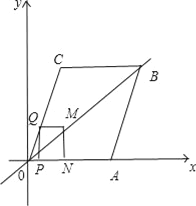
①当0＜t≤6，，，，，
若，则，，
若，则，，
②当6＜t≤8，，，，，
若，则，t=0（舍），
若，则，t3=8；
③8＜t≤10，不存在符合条件的t值．
