题目内容
【题目】如图，矩形OABC中，A（1，0），C（0，2），双曲线y= 
（0＜k＜2）的图象分别交AB，CB于点E，F，连接OE，OF，EF，S△OEF=2S△BEF ， 则k值为（ ）
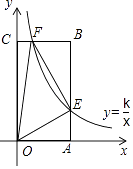
A.
B.1
C.
D.
【答案】A
【解析】解：∵四边形OABC是矩形，BA⊥OA，A（1，0），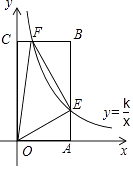 
∴设E点坐标为（1，m），则F点坐标为（ 
，2），
则S△BEF= 
（1﹣ ）（2﹣m），S△OFC=S△OAE= m，
∴S△OEF=S矩形ABCO﹣S△OCF﹣S△OEA﹣S△BEF=2﹣ m﹣ m﹣ （1﹣ ）（2﹣m），
∵S△OEF=2S△BEF，
∴2﹣ m﹣ m﹣ （1﹣ ）（2﹣m）=2 （1﹣ ）（2﹣m），
整理得 
（m﹣2）2+m﹣2=0，解得m1=2（舍去），m2= 
，
∴E点坐标为（1， ）；
∴k= ，
所以答案是：A．
【考点精析】根据题目的已知条件，利用比例系数k的几何意义的相关知识可以得到问题的答案，需要掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积．
练习册系列答案
相关题目
