Question

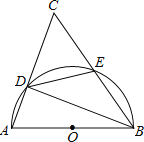
【题目】如图，以的一边为直径的半圆与其它两边，的交点分别为，，且.

（1）试判断的形状，并说明理由.

（2）已知半圆的半径为5，，求的长.

Answer 1

【答案】（1）为等腰三角形．理由见解析；（2）．

【解析】

（1）连结AE，如图，根据圆周角定理，由得∠DAE=∠BAE，由AB为直径得∠AEB=90°，根据等腰三角形的判定方法即可得△ABC为等腰三角形；

（2）由等腰三角形的性质得BE=CE=BC=6，再在Rt△ABE中利用勾股定理计算出AE=8，接着由AB为直径得到∠ADB=90°，则可利用面积法计算出BD的值.

（1）为等腰三角形．

理由如下：

连结，如图，

∵，

∴，即平分，

∵为直径，

∴，

∴，

∴为等腰三角形；

（2）∵为等腰三角形，，

∴，

在中，∵，，

∴，

∵为直径，

∴，

∴，

∴