Question

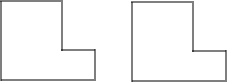
（1）如图，一块方角形的木板，能不能在图中画出一条直线，将其分成面积相等的两部分，（不写作法，在图中直接画出来）；
（2）观察下列各式，你有什么发现．
3²=4+5，5²=12+13，7²=24+25，9²=40+41，…这到底是巧合，还是有什么规律．请你结合有关知识进行研究，如果13²=b+c，则b、c的值可能是多少．

Answer 1

分析：（1）先将图形分割成两个矩形，找出各自的对称中心，过两个对称中心做直线即可；
（2）认真观察三个数之间的关系：首先发现每一组的三个数为勾股数，第一个数为从3开始连续的奇数，第二、三个数为连续的自然数；进一步发现第一个数的平方是第二、三个数的和；最后得出第n组数为（2n+1），（

(2n+1)2-1

2

）（

(2n+1)2+1

2

），由此规律解决问题．

解答：解：（1）如图所示：


（2）∵在3²=4+5中，4=

32-1

2

，5=

32+1

2

；
在5²=12+13中，12=

52-1

2

，13=

52+1

2

；
…
∴在13、b、c中，b=

132-1

2

=84，c=

132+1

2

=85．

点评：此题主要考查了数字变化规律，根据已知认真观察各式的特点，总结规律第n组数为（2n+1），（

(2n+1)2-1

2

）（

(2n+1)2+1

2

）是解题关键．