题目内容
 菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=
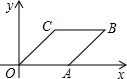
菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC= ,则点B的坐标为 .
,则点B的坐标为 .
【答案】分析:过C作CE⊥OA,根据“∠AOC=45°,OC=2 ”可以求出CE、OE的长,点B的坐标便不难求出.
”可以求出CE、OE的长,点B的坐标便不难求出.
解答:解:过C作CE⊥OA于E,

∵∠AOC=45°,OC=2 ,
,
∴OE=OCcos45°= ,
,
CE=OCsin45°=2,
∴点B的坐标为(2 +2,2).
+2,2).
点评:作辅助线构造直角三角形,根据三角函数求出C点坐标是解本题的关键.
 ”可以求出CE、OE的长,点B的坐标便不难求出.
”可以求出CE、OE的长,点B的坐标便不难求出.解答:解:过C作CE⊥OA于E,

∵∠AOC=45°,OC=2
 ,
,∴OE=OCcos45°=
 ,
,CE=OCsin45°=2,
∴点B的坐标为(2
 +2,2).
+2,2).点评:作辅助线构造直角三角形,根据三角函数求出C点坐标是解本题的关键.

练习册系列答案
相关题目
 菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC=
菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC= (2013•瑶海区一模)每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.
(2013•瑶海区一模)每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示. 秒
秒 如图,菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=
如图,菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=