��Ŀ����
�Ķ�����
��ͼ�٣���ABC���DEF���ǵ���ֱ�������Σ���ACB=��EDF=90�㣬�ҵ�D��AB���ϣ�AB��EF���е��ΪO������BF��CD��CO����Ȼ��C��F��O��ͬһ��ֱ���ϣ�����֤����BOF�ա�COD����BF=CD��
�������
��1����ͼ���е�Rt��DEF�Ƶ�O��ת�õ�ͼ�ڣ������ʱ�߶�BF��CD��������ϵ����֤����Ľ��ۣ�
��2����ͼ�ۣ�����ABC���DEF���ǵȱ������Σ�AB��EF���е��ΪO��������1���еĽ�����Ȼ�����������������˵�����ɣ��粻�����������BF��CD֮���������ϵ��
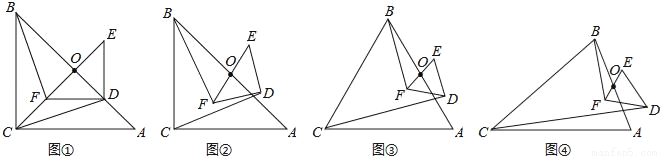
��3����ͼ�ܣ�����ABC���DEF���ǵ��������Σ�AB��EF���е��Ϊ0���Ҷ��ǡ�ACB=��EDF=������ֱ��д��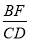 ��ֵ���ú�����ʽ�ӱ�ʾ������
��ֵ���ú�����ʽ�ӱ�ʾ������
��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ

 B.
B. 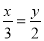 C.
C. 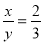 D.
D. 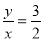
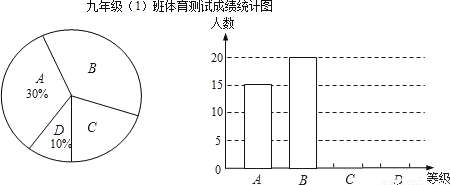
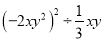 ��2��
��2��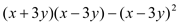
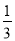 ���෴���ǣ�������
���෴���ǣ�������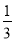 B. -
B. -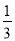 C. 3 D. -3
C. 3 D. -3