��Ŀ����
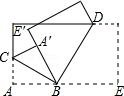
����Ŀ����֪��������ABCD�ı߳�Ϊ![]() ���ף��Խ���AC�ϵ���������E,F����E�ӵ�A����F�ӵ�Cͬʱ�������ضԽ�����1����/�����ͬ�ٶ��˶�����E��EH��AC��Rt��ACD��ֱ�DZ���H����F��FG��AC��Rt��ACD��ֱ�DZ���G������HG��EB����HE��EF��FG��GHΧ�ɵ�ͼ�����Ϊ
���ף��Խ���AC�ϵ���������E,F����E�ӵ�A����F�ӵ�Cͬʱ�������ضԽ�����1����/�����ͬ�ٶ��˶�����E��EH��AC��Rt��ACD��ֱ�DZ���H����F��FG��AC��Rt��ACD��ֱ�DZ���G������HG��EB����HE��EF��FG��GHΧ�ɵ�ͼ�����Ϊ![]() ��AE��EB��BAΧ�ɵ�ͼ�����Ϊ
��AE��EB��BAΧ�ɵ�ͼ�����Ϊ![]() ������涨���߶ε����Ϊ
������涨���߶ε����Ϊ![]() ����E����C,F����Aֹͣ����E���˶�ʱ��Ϊx�룬����������⣺
����E����C,F����Aֹͣ����E���˶�ʱ��Ϊx�룬����������⣺
��1����ͼ�٣��ж��ı���EFGH��ʲô�ı��Σ���֤����
��2����0<x<8ʱ����xΪ��ֵʱ��![]() ��
��
��3����![]() ��
��![]() �ĺͣ�����x�Ĵ���ʽ��ʾy����ͼ��Ϊ����ͼ��
�ĺͣ�����x�Ĵ���ʽ��ʾy����ͼ��Ϊ����ͼ��


���𰸡���1���ı���EFGH�Ǿ��Σ�֤������������2��6����3��![]()
��������(1)�����ȸ��ݶ���E��F���˶��ٶ����˶�ʱ�����ͬ�ó�AE=CF�����������ε����ʼ���֪EH��AC��FG��AC�ó���CGF���AHE���ǵ���ֱ�������Σ�Ȼ�������һ������ֱ�ǵ�ƽ���ı����Ǿ��εó����ۣ�(2)�������ɹ��ɶ������������ABCD�ĶԽ��߳�Ϊ16��������BD��AC��O����BO=8��Ȼ���ú�x�Ĵ���ʽ�ֱ��ʾS1��S2����S1=S2ʱ�ó�����x�ķ��̣��ⷽ�̼��ɣ�(3)����Ϊ��x=8ʱ����E���F�غϣ���ʱS1=0��y=S2����Ӧ��0��x��8��8��x��16����������ۣ�
(1)���ı���EFGH�Ǿ��Σ�
֤������E��F�˶�ʱ����ͬ����AE=CF����![]() ��
��![]() ��
��![]() ��
��![]() ����EH//FG ��
����EH//FG ��
��ABCD��������AD=DC����D=900�����GCF=��HAE=450��
��![]() ��
��![]() ��
��![]() ��
��![]() �����CGF=��AHE=450�����GCF=��CGF����HAE=��AHE
�����CGF=��AHE=450�����GCF=��CGF����HAE=��AHE
��AE=EH��CF=FG����EH=FG �����ı���EFGH��ƽ���ı��Σ�
��![]() ��
��![]() �����ı���EFGH�Ǿ��Σ�
�����ı���EFGH�Ǿ��Σ�
(2)��![]() �����α߳�Ϊ
�����α߳�Ϊ![]() ��
��![]() ��
��
![]() ����
����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��![]() �����
�����![]() ����ȥ����
����ȥ����![]() ��
�� ![]() ��
��![]() ʱ��
ʱ��![]() ��
��

(3)���ٵ�![]() ʱ��
ʱ��![]() ��
��
�ڵ�![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() ��
��
![]() ��
�� ![]() ��
��

 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�����Ŀ��ij����һ�ܼƻ�ÿ������ij��Ʒ100�֣����ڹ���ʵ�����ݣ�ÿ���ϰ�������һ����ȣ�ʵ��ÿ����������ƻ������������±����Լƻ���Ϊ�������ӵĶ�����Ϊ���������ٵĶ�����Ϊ������
���� | һ | �� | �� | �� | �� | �� | �� |
����/�� | ��1 | +3 | ��2 | +4 | +7 | ��5 | ��10 |
��1������������һ������������ٵ�һ����������ٶ֣�
��2���������������Ƕ��ٶ֣���ԭ�ƻ������˻��Ǽ����ˣ�������Ϊ���ٶ֣�
��3���������������IJ�Ʒȫ����35������һ����װ�������뿪��������ƽ��ÿ��������Լ��װ�ض��ٶ֣��������ȷ��0.01�֣�