题目内容
已知△ABC中,AC=BC=8,∠ACB=90°,D是直线AC上一点,CD:AC=1:2,折叠△ABC,使B落在D点上,则折痕长为 .

试题分析:已知△ABC中,AC=BC=8,∠ACB=90°,D是直线AC上一点,CD:AC=1:2,则CD=
 ;折叠△ABC,使B落在D点上,设BC上的一点为E,AB上形成的一点为F;在三角形CDE中∠ACB=90°,设DE="x,CE=8-x;" 由勾股定理得
;折叠△ABC,使B落在D点上,设BC上的一点为E,AB上形成的一点为F;在三角形CDE中∠ACB=90°,设DE="x,CE=8-x;" 由勾股定理得 ,解得x=
,解得x= ;根据折叠过程三角形DEF为等腰直角三角形EF=DE=
;根据折叠过程三角形DEF为等腰直角三角形EF=DE=
点评:本题考查折叠的知识,考生要掌握折叠的性质,在折叠过程中折叠后与折叠前边的关系是解本题的关键

练习册系列答案
相关题目
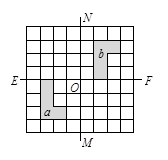
 )时,设一直角边与x轴交于点E,另一直角边与y轴交于点F,在三角板绕点P旋转的过程中,使得△POE能否成为等腰三角形.请写出所有满足条件的点F的坐标 。
)时,设一直角边与x轴交于点E,另一直角边与y轴交于点F,在三角板绕点P旋转的过程中,使得△POE能否成为等腰三角形.请写出所有满足条件的点F的坐标 。

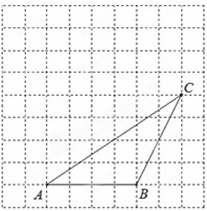
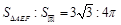 ,以上结论正确的有( )
,以上结论正确的有( )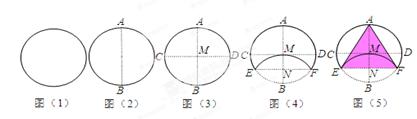
 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么 的度数为 。
的度数为 。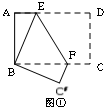
 经过怎样的平移得到
经过怎样的平移得到 ( )
( )
