题目内容
如图，?ABCD的对角线相交于点O，且AC⊥AB，OC=3cm，OB=6cm．
求AB的长及?ABCD的面积．
解：∵四边形ABCD是平行四边形，
∴OA=OC=3，AC=6，
∵AC⊥AB，OB=6，
∴
．
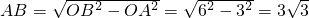则?ABCD的面积为AB•AC=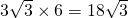
．
∴AB的长为
cm，?ABCD的面积为
cm2．
分析：由已知四边形ABCD是平行四边形，可得AO=0C=3，AC=6，又已知AC⊥AB，所以由勾股定理可求出AB，从而求出?ABCD的面积．
点评：此题考查的知识点是平行四边形的性质及勾股定理的应用，关键是运用平行四边形的性质得出AO及AC，再由勾股定理求出AB．
∴OA=OC=3，AC=6，
∵AC⊥AB，OB=6，
∴
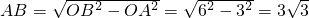．则?ABCD的面积为AB•AC=
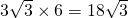．∴AB的长为
cm，?ABCD的面积为cm2．分析：由已知四边形ABCD是平行四边形，可得AO=0C=3，AC=6，又已知AC⊥AB，所以由勾股定理可求出AB，从而求出?ABCD的面积．
点评：此题考查的知识点是平行四边形的性质及勾股定理的应用，关键是运用平行四边形的性质得出AO及AC，再由勾股定理求出AB．
练习册系列答案
期末集结号系列答案
相关题目
如图，?ABCD的两条对角线AC、BD相交于点O，问图中全等的三角形有哪几对？
如图，?ABCD的两条对角线AC、BD相交于点O，那么，图中有几对三角形全等（ ）
如图，?ABCD的两条对角线AC，BD相交于点O，则图中全等的三角形有（ ）对．