Question

如图，在直角坐标系中，四边形OABC是直角梯形，BC∥OA，⊙P分别与OA、OC、BC相切于点E、D、B，与AB交于点F．已知A（3+2，0），B（3，6），则∠FDE=________．

Answer 1

30°
分析：连接PB、PE．由⊙P分别与OA、OC、BC相切于点E、D、B，与AB交于点F．易得B、P、E在一条直线上，易求得ZE与BE的长，则可求得∠ABE的度数，又由圆周角定理，即可求得答案．
解答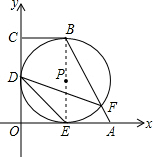：解：连接PB、PE．
∵⊙P分别与OA、BC相切于点E、B，
∴PB⊥BC，PE⊥OA，
∵BC∥OA，
∴B、P、E在一条直线上，
∵四边形OABC是直角梯形，BC∥OA，
∴四边形BCOE是矩形，
∴OE=BC，BE=OC，
∵A（3+2，0），B（3，6），
∴AE=2，BE=6，
∴tan∠ABE==，
∴∠ABE=30°，
∴∠FDE=∠ABE=30°．
故答案为：30°．
点评：此题考查了切线的性质、圆周角定理以及直角梯形的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．