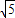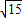题目内容
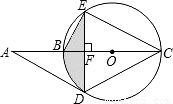
(2010•江北区模拟)如图,点A为⊙O直径CB延长线上一点,过点A作⊙O的切线AD,切点为D,过点D作DE⊥AC,垂足为F,连接BE、CD、CE,已知∠BED=30°.(1)求tanA的值;
(2)若AB=2,试求CE的长.
(3)在(2)的条件下,求图中阴影部分的面积.
【答案】分析:(1)连接OD,根据切线的性质,∠ADO=90°,从而易证∠BOD=60°,所以∠A是特殊角等于30°,所以sinA= .
.
(2)求弦长,要作弦的弦心距,构造直角三角形,并利用(1)的结论,求出圆的半径,从而求出弦长.
(3)通过证明△BEF≌△ODF,将阴影部分不规则图形的面积转化为规则图形的面积,也就是扇形BOD的面积.
解答:解:(1)连接OD,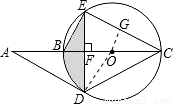
∵DA为⊙O的切线,切点为D,
∴OD⊥AD,∠ADO=90°,
又∵∠BED=30°,
∴∠BOD=60°,
∴∠A=30°,
∴tanA=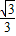 .
.
(2)过点O作OG⊥EC于点G
∴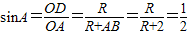 ,
,
得R=2,
∴OC=2,
∵DE⊥AC,BC为直径,
∴弧BE=弧BD,
∴∠ECB=∠BED=30°,
∴CE=2CG=2•OCcos30°=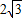 .
.
(3)∵由(1)∠BOD=60°得∠ODF=30°,
∴OF= OD=
OD= OB,即OF=FB,
OB,即OF=FB,
由DE⊥AC,BC为直径,
得EF=FD,∠OFD=∠BFE=90°,
∴△BEF≌△ODF,
∴阴影部分面积等于扇形BOD的面积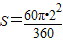 =
=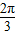 .
.
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.
 .
.(2)求弦长,要作弦的弦心距,构造直角三角形,并利用(1)的结论,求出圆的半径,从而求出弦长.
(3)通过证明△BEF≌△ODF,将阴影部分不规则图形的面积转化为规则图形的面积,也就是扇形BOD的面积.
解答:解:(1)连接OD,

∵DA为⊙O的切线,切点为D,
∴OD⊥AD,∠ADO=90°,
又∵∠BED=30°,
∴∠BOD=60°,
∴∠A=30°,
∴tanA=
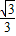 .
.(2)过点O作OG⊥EC于点G
∴
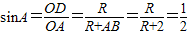 ,
,得R=2,
∴OC=2,
∵DE⊥AC,BC为直径,
∴弧BE=弧BD,
∴∠ECB=∠BED=30°,
∴CE=2CG=2•OCcos30°=
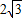 .
.(3)∵由(1)∠BOD=60°得∠ODF=30°,
∴OF=
 OD=
OD= OB,即OF=FB,
OB,即OF=FB,由DE⊥AC,BC为直径,
得EF=FD,∠OFD=∠BFE=90°,
∴△BEF≌△ODF,
∴阴影部分面积等于扇形BOD的面积
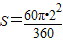 =
=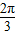 .
.点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(2010•江北区模拟)阅读下列方法:为了找出序列3、8、15、24、35、48、…的规律,我们有一种“因式分解法”.如下
表:

因此,我们得到第n项是n(n+2),请你利用上述方法,说出序列:0、5、12、21、32、45、…的第n项是 .
表:
| 项 | 1 | 2 | 3 | 4 | 5 | 6 | … | n |
| 值 | 3 | 8 | 15 | 24 | 35 | 48 | … |

因此,我们得到第n项是n(n+2),请你利用上述方法,说出序列:0、5、12、21、32、45、…的第n项是 .
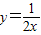 图象在第一象限的分支上的任意一点,P点坐标为(a,b),由点P分别向x轴,y轴作垂线PM、PN,垂足分别为M、N;PM、PN分别与直线交于点E,点F.
图象在第一象限的分支上的任意一点,P点坐标为(a,b),由点P分别向x轴,y轴作垂线PM、PN,垂足分别为M、N;PM、PN分别与直线交于点E,点F.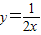 上是否存在点P,使点P到直线AB的距离最短的点,若存在,请求出点P的坐标及最短距离;若不存在,说明理由
上是否存在点P,使点P到直线AB的距离最短的点,若存在,请求出点P的坐标及最短距离;若不存在,说明理由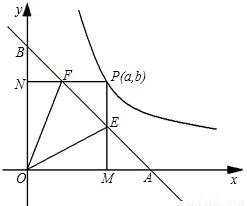
 的对称轴是直线x=1,且经过点P(3,0),抛物线的解析式是 .
的对称轴是直线x=1,且经过点P(3,0),抛物线的解析式是 .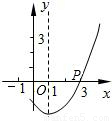
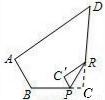
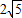 米,那么两树间的水平距离为( )米.
米,那么两树间的水平距离为( )米.