题目内容
如图，三角形ABC的面积为1，BD：DC=2：1，E为AC的中点，AD与BE相交于P，那么四边形PDCE的面积为______．
连接CP，
设△CPE的面积是x，△CDP的面积是y．
∵BD：DC=2：1，E为AC的中点，
∴△BDP的面积是2y，△APE的面积是x，
∵BD：DC=2：1，CE：AC=2：1，
∴△ABP的面积是4x．
∴4x+x=2y+x+y，
解得y=
x．
又∵4x+x=
，
x=
．
则四边形PDCE的面积为x+y=
．
故答案为：
．
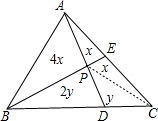
设△CPE的面积是x，△CDP的面积是y．
∵BD：DC=2：1，E为AC的中点，
∴△BDP的面积是2y，△APE的面积是x，
∵BD：DC=2：1，CE：AC=2：1，
∴△ABP的面积是4x．
∴4x+x=2y+x+y，
解得y=
| 4 |
| 3 |
又∵4x+x=
| 1 |
| 2 |
x=
| 1 |
| 10 |
则四边形PDCE的面积为x+y=
| 7 |
| 30 |
故答案为：
| 7 |
| 30 |
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
