题目内容
P为半径为R的⊙O内一点,Q为射线OP上一点,如果满足OP•OQ=R2,则称P、Q两点为⊙O互为反演点.已知:E、B两点及A、F两点分别为⊙O的互为反演点.(1)求证:△OEF∽△OAB;
(2)△OAB中,∠O、∠A、∠B所对的边分别为c、a、b关于x的方程(a-b)x2-2cx+a+b=0有两个相等的实数根,延长FE与⊙O相交于D点,求证:BD是⊙O的切线.

分析:(1)根据已知得出OE•OB=OA•OF,再利用相似三角形的判定,即可得出△OEF∽△OAB;
(2)利用△=(-2c)2-4(a-b)(a+b)=0,得出∠A的度数,再利用OE•OB=R2,得出△ODE∽△OBD,从而得出证明方法.
(2)利用△=(-2c)2-4(a-b)(a+b)=0,得出∠A的度数,再利用OE•OB=R2,得出△ODE∽△OBD,从而得出证明方法.
解答: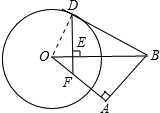 解:(1)∵E、B两点及A、F两点分别为⊙O的互为反演点,
解:(1)∵E、B两点及A、F两点分别为⊙O的互为反演点,
∴OE•OB=OA•OF,
∴
=
,
∵∠EOF=∠AOB,
∴△OEF∽△OAB;
(2)连接OD,
∵关于x的方程(a-b)x2-2cx+a+b=0有两个相等的实数根,
∴△=(-2c)2-4(a-b)(a+b)=0,
即c2+b2=a2,
∴∠A=90°,
∵△OEF∽△OAB,
∴∠A=∠OEF=90°,
∵OE•OB=R2,
∴
=
,
∵∠DOE=∠BOD,
∴△ODE∽△OBD,
∴∠ODB=∠OED=90°,
∴BD是⊙O的切线.
 解:(1)∵E、B两点及A、F两点分别为⊙O的互为反演点,
解:(1)∵E、B两点及A、F两点分别为⊙O的互为反演点,∴OE•OB=OA•OF,
∴
| OE |
| OA |
| OF |
| OB |
∵∠EOF=∠AOB,
∴△OEF∽△OAB;
(2)连接OD,
∵关于x的方程(a-b)x2-2cx+a+b=0有两个相等的实数根,
∴△=(-2c)2-4(a-b)(a+b)=0,
即c2+b2=a2,
∴∠A=90°,
∵△OEF∽△OAB,
∴∠A=∠OEF=90°,
∵OE•OB=R2,
∴
| R |
| EO |
| BO |
| R |
∵∠DOE=∠BOD,
∴△ODE∽△OBD,
∴∠ODB=∠OED=90°,
∴BD是⊙O的切线.
点评:此题主要考查了根的判别式以及相似三角形的判定与性质、切线的判定等知识,根据已知得出OE•OB=R2从而得出相似三角形是解决问题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 能用一句话归纳你的发现吗?
能用一句话归纳你的发现吗?
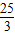 ,求PC、PD的长.
,求PC、PD的长.