Question

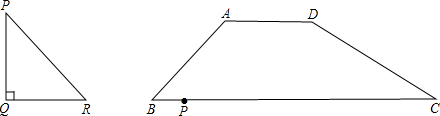
如图，Rt△PQR中，∠PQR=90°，当PQ=RQ时，PR=

2

PQ．根据这个结论，解决下面问题：在梯形ABCD中，∠B=45°，AD∥BC，AB=5，AD=4，BC=8

3

，P是线段BC上一动点，点P从点B出发，以每秒

2

个单位的速度向C点运动．

（1）当BP=

8

3

-4

时，四边形APCD为平行四边形；
（2）求四边形ABCD的面积；
（3）设P点在线段BC上的运动时间为t秒，当P运动时，△APB可能是等腰三角形吗？如能，请求出t的值；如不能，请说明理由．

Answer 1

分析：（1）根据当AD=PC=4时，四边形APCD为平行四边形，利用BP=BC-PC求出即可；
（2）首先求出AE的长，再利用S_{四边形ABCD}=

1

2

（AD+BC）×AE即可得出答案；
（3）利用①当AP=BP时，②当AB=BP时，③当AB=AP时，分别求出时间即可．

解答：解：（1）根据题意可得出：当AD=PC=4时，四边形APCD为平行四边形；
∴BP=BC-PC=8

3

-4时，四边形APCD为平行四边形；
故答案为：8

3

-4；

（2）作AE⊥BC于点E，
∴∠AEB=90°，
∵∠A=45°，
∴AE=BE，
∴AB=

2

AE，
∵AB=5，
∴AE=

5

2

2

，
∴S_{四边形ABCD}=

1

2

（AD+BC）×AE=

1

2

（4+8

3

）×

5

2

2

=5

2

+10

6

，；

（3）①当AP=BP时，由（2）知：BP=

5

2

2

，
∴t=

5

2

2

÷

2

=

5

2

（秒），
②当AB=BP时，由题意可得：BP=5，
∴t=5÷

2

=

5

2

2

（秒），
③当AB=AP时，
由题意可得：BP=

2

AB=5

2

，
∴t=5

2

÷

2

=5（秒），
综上所述：当t=

5

2

秒，

5

2

2

秒，5秒时，△ABP是等腰三角形．

点评：此题主要考查了四边形综合应用以及等腰三角形的性质和四边形面积求法等知识，利用分类讨论得出是解题关键．