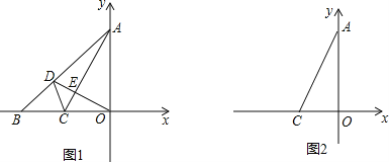题目内容
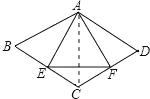
【题目】如图，菱形
中，
分别是
的中点，连接
，则
的周长为（ ）
A.
B.
C.
D.
【答案】D
【解析】
首先根据菱形的性质证明△ABE≌△ADF，然后连接AC可推出△ABC以及△ACD为等边三角形．根据等边三角形三线合一的性质又可推出△AEF是等边三角形．根据勾股定理可求出AE的长，继而求出周长．
解：∵四边形ABCD是菱形，
∴AB＝AD＝BC＝CD＝2cm，∠B＝∠D，
∵E、F分别是BC、CD的中点，
∴BE＝DF，
在△ABE和△ADF中，
，
∴△ABE≌△ADF（SAS），
∴AE＝AF，∠BAE＝∠DAF．
连接AC，
∵∠B＝∠D＝60°，
∴△ABC与△ACD是等边三角形，
∴AE⊥BC，AF⊥CD，
∴∠BAE＝∠DAF＝30°，
∴∠EAF＝60°，BE=
AB=1cm，
∴△AEF是等边三角形，AE＝
，
∴周长是
．
故选：D．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
