题目内容
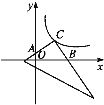
【题目】一直角三角形放置在如图所示的平面直角坐标系中,直角顶点C刚好落在反比例函数y=
的图象的一支上,两直角边分别交y、x轴于A、B两点.当CA=CB时,四边形CAOB的面积为( )
A. 4 B. 8 C. 2
D. 
【答案】B
【解析】
作CE垂直x轴于点E，AF⊥CE于点F，CM垂直于y轴于点M，AC交x轴于点N，求出△AFC≌△CEB得到AF=CE=2
，再利用四边形CAOB的面积=正方形MOEC的面积即可得答案．
作CE垂直x轴于点E，AF⊥CE于点F，CM垂直于y轴于点M，AC交x轴于点N，
∵∠NOA=∠NCB=90°，∠ANO=∠BNC，
∴△ANO∽△CNB，
∴∠NAO=∠NBC，
又∵AO∥CE，
∴∠NAO=∠ACF，
∴∠ACF=∠NBC，即∠ACF=∠EBC
∵∠AFC=∠CEB=90°，AC=CB，∠ACF＝∠EBC，
∴△AFC≌△CEB（AAS）
∵四边形MAFC是矩形，
∴△AFC≌△MAC，
∴△CEB≌△MAC，
∴S△CEB=S△MAC，
∴AF=CE，
∵AF=CM
∴CM=BE
∴C点的横坐标与纵坐标相等，
∵点C在反比例函数y=
的图像上，
∴AF×CE=8，
∴AF=CE=2
∵S四边形CAOB=S四边形CAOE+S△CEB= S四边形CAOE+S△MAC=S正方形MOEC=(2)2=8.
故选B.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】有这样一个问题：探究函数y＝
的图象与性质．小彤根据学习函数的经验，对函数y＝的图象与性质进行了探究．
下面是小彤探究的过程，请补充完整：
(1)函数y＝的自变量x的取值范围是 ；
(2)下表是y与x的几组对应值：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | … |
y | … |
| m |
| 0 | ﹣1 | 3 | 2 |
|
|
| … |
则m的值为 ；
(3)如图所示，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出了图象的一部分，请根据剩余的点补全此函数的图象；
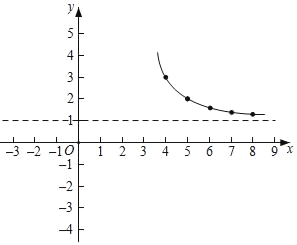
(4)观察图象，写出该函数的一条性质 ；
(5)若函数y＝的图象上有三个点A(x1，y1)、B(x2，y2)、C(x3，y3)，且x1＜3＜x2＜x3，则y1、y2、y3之间的大小关系为 ；
