题目内容
已知△ABC为锐角三角形，AD、BE是两条高，S△ABC=18，S△DEC=2，
，则△ABC的外接圆的直径长为________．
9
分析：利用三角形的相似比与面积比的关系，可求出AB，再利用圆周角定理得出∠F=∠C，再利用三角函数关系可求出．
解答：
解：作△ABC外接⊙O的直径AF，连接BF，
∵AD、BE是两条高，
∴△DEC∽△ABC，
∴
，
∴
=
，
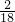AB=6
，
∴cosC=
=
，
sinC=
，
于是AF=
．
故答案为：9．
点评：此题主要考查了相似三角形的性质，以及圆周角定理和三角函数定理，题目比较典型．
分析：利用三角形的相似比与面积比的关系，可求出AB，再利用圆周角定理得出∠F=∠C，再利用三角函数关系可求出．
解答：
解：作△ABC外接⊙O的直径AF，连接BF，∵AD、BE是两条高，
∴△DEC∽△ABC，
∴
，∴
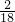=，AB=6
，∴cosC=
=，sinC=
，于是AF=
．故答案为：9．
点评：此题主要考查了相似三角形的性质，以及圆周角定理和三角函数定理，题目比较典型．
练习册系列答案
相关题目