题目内容
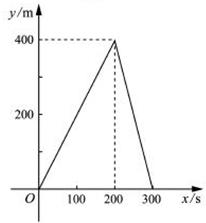
14、甲、乙两同学同时从400m环形跑道上的同一点出犮,同向而行.甲的速度为6m/s,乙的速度为4m/s.设经过x(单位:s)后,跑道上此两人间的较短部分的长度为y(单位:m).则y与x(0≤x≤300)之间的函数关系可用图象表示为( )
分析:由于相向而行,且二人速度差为6-4=2m/s,二人间最长距离为200米,最短距离为0,据此即可进行推理.
解答:解:二人速度差为6-4=2m/s,
100秒时,二人相距2×100=200米,
200秒时,二人相距2×200=400米,较短部分的长度为0,
300秒时,二人相距2×300=600米,即甲超过乙600-400=200米.
由于y=2x或y=400-2x,函数图象为直线(线段).
故选C.
100秒时,二人相距2×100=200米,
200秒时,二人相距2×200=400米,较短部分的长度为0,
300秒时,二人相距2×300=600米,即甲超过乙600-400=200米.
由于y=2x或y=400-2x,函数图象为直线(线段).
故选C.
点评:本题考查利用函数的图象解决实际问题,正确理解函数图象表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
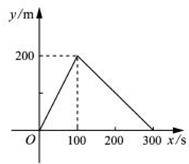 (B)
(B)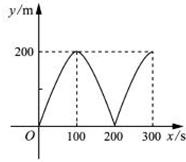
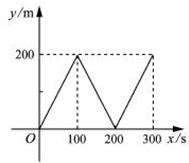 (D)
(D)