题目内容
如图，函数y=x+2与y轴交于点A，与y=x2交于点B，求A、B两点坐标，并求出△OAB的面积．
解：把x=0代入y=x+2，得y=2，
∴A的坐标为（0，2）；
联立
，
解得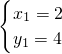
或
（舍去）；
∴B的坐标为（2，4），
∴S△OAB=
×2×2=2．
分析：根据直线AB的解析式可求得点A的坐标，联立抛物线的解析式可得到点B的坐标，以OA为底，B点横坐标的绝对值为高，可求得△OAB的面积．
点评：此题考查了函数图象与坐标轴交点坐标的求法、函数图象交点坐标的求法以及三角形面积的计算方法，属于基础知识，难度不大．
∴A的坐标为（0，2）；
联立
，解得
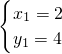或（舍去）；∴B的坐标为（2，4），
∴S△OAB=
×2×2=2．分析：根据直线AB的解析式可求得点A的坐标，联立抛物线的解析式可得到点B的坐标，以OA为底，B点横坐标的绝对值为高，可求得△OAB的面积．
点评：此题考查了函数图象与坐标轴交点坐标的求法、函数图象交点坐标的求法以及三角形面积的计算方法，属于基础知识，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
如图：函数y=-kx（k≠0）与y=-
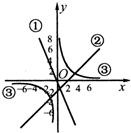如图，函数图象①、②、③的表达式应为（ ）A、y=-
| ||||
B、y=
| ||||
C、y=-
| ||||
D、y=-
|
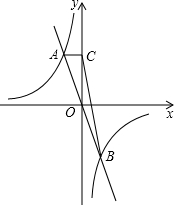如图，函数y=-kx与
如图，函数y1=k1x+b的图象与函数y2=