题目内容
下列判定三角形全等的定理中,能够直接或间接证明两个等腰直角三角形全等的有
①SSS;②SAS;③AAS;④SSA;⑤ASA;⑥HL.
- A.3个
- B.4个
- C.5个
- D.6个
D
分析:分别根据全等三角形的判定方法由两个等腰直角三角形的性质,分别假设已知条件证明即可.
解答: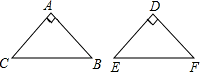 解:∵△ACB和△DEF是两个等腰直角三角形,
解:∵△ACB和△DEF是两个等腰直角三角形,
∴∠A=∠D=90°,AC=AB,DE=DF,
当AC=DE,AB=DF,BC=EF,
∴ ,
,
∴△ACB≌△DEF(SSS);故选项①正确;
∵△ACB和△DEF是两个等腰直角三角形,
∴当∠C=∠B=45°,∠E=∠F=45°,
∵AC=DE,AB=DF,
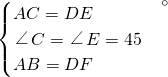 ,
,
∴△ACB≌△DEF(SAS),故选项②正确;
∵△ACB和△DEF是两个等腰直角三角形,
∴当∠C=∠B=45°,∠E=∠F=45°,
∵AC=DE,
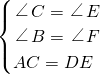 ,
,
∴△ACB≌△DEF(AAS),故选项③正确;
∵△ACB和△DEF是两个等腰直角三角形,
∴当∠C=∠E=45°,AC=DE,AB=DF,
 ,
,
∴△ACB≌△DEF(SSA),故选项④正确;
∵△ACB和△DEF是两个等腰直角三角形,
∴当∠C=∠E=45°,∠A=∠D=90°,AC=DE,
 ,
,
∴△ACB≌△DEF(ASA),故选项⑤正确;
∵△ACB和△DEF是两个等腰直角三角形,
∴当∠A=∠D=90°,AC=DE,BC=EF,
在Rt△ACB和Rt△DEF中,
 ,
,
∴Rt△ACB≌Rt△DEF(HL),故选项⑥正确;
故①②③④⑤⑥都正确一共6个.
故选:D.
点评:此题主要考查了全等三角形的判定方法的应用,由两个等腰直角三角形得出已知条件进而判定得出是解题关键.
分析:分别根据全等三角形的判定方法由两个等腰直角三角形的性质,分别假设已知条件证明即可.
解答:
 解:∵△ACB和△DEF是两个等腰直角三角形,
解:∵△ACB和△DEF是两个等腰直角三角形,∴∠A=∠D=90°,AC=AB,DE=DF,
当AC=DE,AB=DF,BC=EF,
∴
 ,
,∴△ACB≌△DEF(SSS);故选项①正确;
∵△ACB和△DEF是两个等腰直角三角形,
∴当∠C=∠B=45°,∠E=∠F=45°,
∵AC=DE,AB=DF,
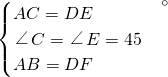 ,
,∴△ACB≌△DEF(SAS),故选项②正确;
∵△ACB和△DEF是两个等腰直角三角形,
∴当∠C=∠B=45°,∠E=∠F=45°,
∵AC=DE,
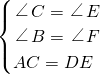 ,
,∴△ACB≌△DEF(AAS),故选项③正确;
∵△ACB和△DEF是两个等腰直角三角形,
∴当∠C=∠E=45°,AC=DE,AB=DF,
 ,
,∴△ACB≌△DEF(SSA),故选项④正确;
∵△ACB和△DEF是两个等腰直角三角形,
∴当∠C=∠E=45°,∠A=∠D=90°,AC=DE,
 ,
,∴△ACB≌△DEF(ASA),故选项⑤正确;
∵△ACB和△DEF是两个等腰直角三角形,
∴当∠A=∠D=90°,AC=DE,BC=EF,
在Rt△ACB和Rt△DEF中,
 ,
,∴Rt△ACB≌Rt△DEF(HL),故选项⑥正确;
故①②③④⑤⑥都正确一共6个.
故选:D.
点评:此题主要考查了全等三角形的判定方法的应用,由两个等腰直角三角形得出已知条件进而判定得出是解题关键.

练习册系列答案
相关题目
