题目内容
如图,已知⊙O1和⊙O2相交于A、B,AC、AD分别是两圆的直径。
(1)C、B、D三点在同一直线吗?为什么?
(2)当⊙O1和⊙O2满足什么条件时,所得图中的△ACD是等腰三角形,请画出示意图。
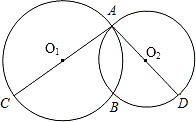
解:(1)连接AB、BC、BD
∵AC、AD是⊙O1和⊙O2的直径
∴∠ABC=90°,∠ABD=90°
∴∠CBD=∠ABC+∠ABD=180°
∴C、B、D三点在同一条直线上;
(2)①当⊙O1与⊙O2的直径相等,即AC=AD时所得图中的△ACD是等腰
三角形;
②当O2在⊙O1上时,
连接CO2∵AC是⊙O1的直径,∴∠AO2C=90°
∴CO2⊥AD
又O2A=O2D
∴CA=CD
于是当O2在⊙O1上时,△ACD是等腰三角形;………(过程2分,图1分,共3分)
③同②当O1在⊙O2上时,可得DA=DC,所得图中的△ACD是等腰三角形.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将抛物线y=(x﹣1)2+3向左平移1个单位,得到的抛物线与y轴的交点坐标是( )
|
| A. | (0,2) | B. | (0,3) | C. | (0,4) | D. | (0,7) |
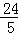 cm;
cm;




 A B C D
A B C D
 ;
;  .
.